Abb. 1-1
Kegelschnitte sind meistens ein wenig umständlich zu
zeichnen.
Unten stelle ich eine einheitliche Teilpunktmethode dar, mit deren Hilfe beliebige Anzahl
der Punkte auf Ellipse, Parabel und Hyperbel sich bestimmen lässt.
Sie ist relativ
einfach in der Anwendung, da die Vorgehensweise in alle Fällen (siehe Beispiele
unten) beinahe gleich ist.
Einige Elemente der Kurven wie Achsen bzw. Durchmesser,
Punkte u. a. sind vorgegeben (die sind weiß gezeichnet).
Entsprechende Strecken werden in beliebig viele gleichen Teilen
untergeteilt.
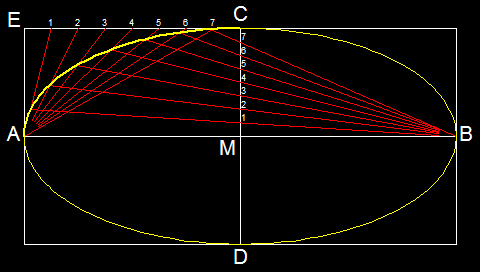
Aus zwei Scheitelpunkten zeichnet man zwei Geradenbüschel, bzw. ein Geradenbüschel und
ein Geradenbündel im Falle der
Parabel, durch die Teilungspunkte (siehe Beispiele).
Die Schnittpunkte entsprechenden Geradenpaaren liegen dann auf den gesuchten Kurven.
Die Teilpunktmethode kann man auch in der Perspektive anwenden z. B. in der Konstruktion des Kreises.
1.1 Beide Achsen sind vorgegeben:

Abb. 1-1
1.2 Zwei konjugierte Durchmesser sind vorgegeben:
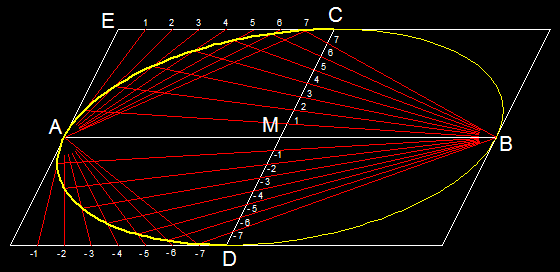
Abb. 1-2
1.3 Ein Durchmesser AB und die Richtung des zweiten, konjugierten Durchmesser bzw. die Tangente im Punkt A, und ein beliebiger Punkt P auf der Ellipse sind vorgegeben:
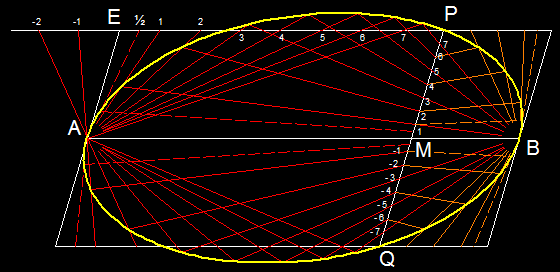
Abb. 1-3
2.1 Eine Achse bzw. ein Durchmesser AB, wobei der Punkt B unendlich weit entfernt ist, die Tangente im Punkt A und ein beliebiger Punkt C der Parabel sind vorgegeben:
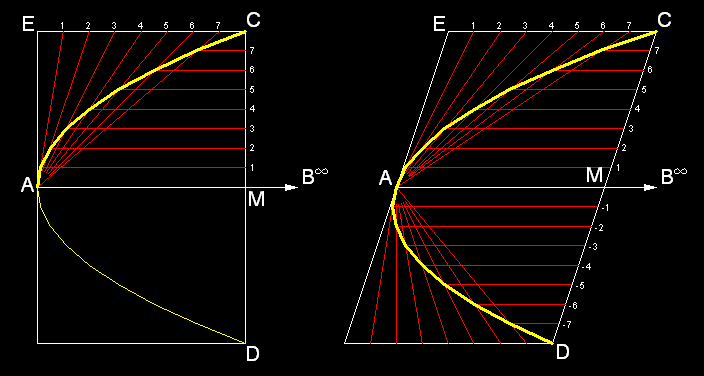
Abb. 2-1
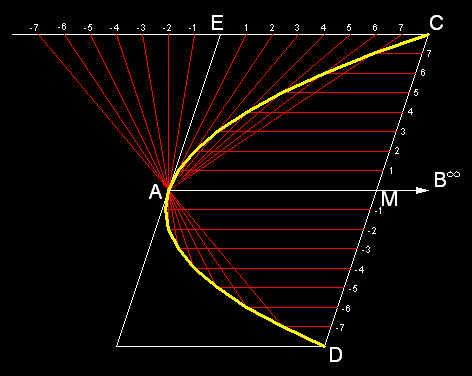
Abb. 2-2
3.1 Eine Achse bzw. ein Durchmesser AB, die Tangente im Punkt A und beliebiger Punkt P der Hyperbel sind vorgegeben:
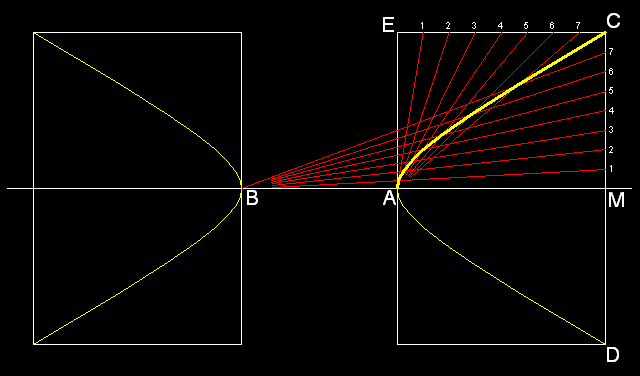
Abb. 3-1
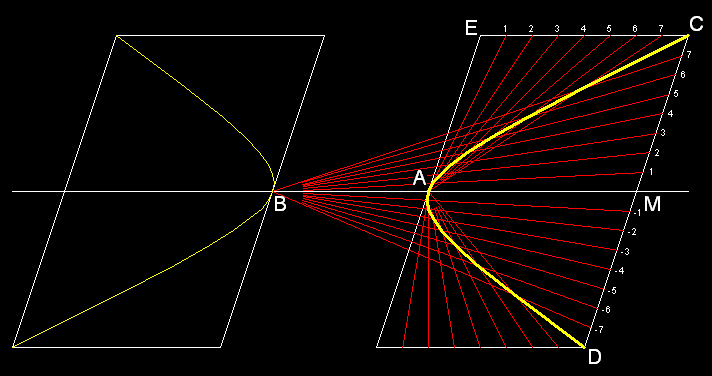
Abb. 3-2
Die Hyperbel hat zwei Asymptoten. Hier wird gezeigt, wie man die bestimmen kann.
______________________________________
PDF-Datei: Hyperbel-Scheitelpunkt
Kegelschnitte als Durchdringungslinie
© Tadeusz E. Dorozinski
Stand: 26.09.2021