Hyperbel - neue Zeichnenmethode

Gegeben sind beide Asymptoten und beide Scheitelpunkte einer Hyperbel.
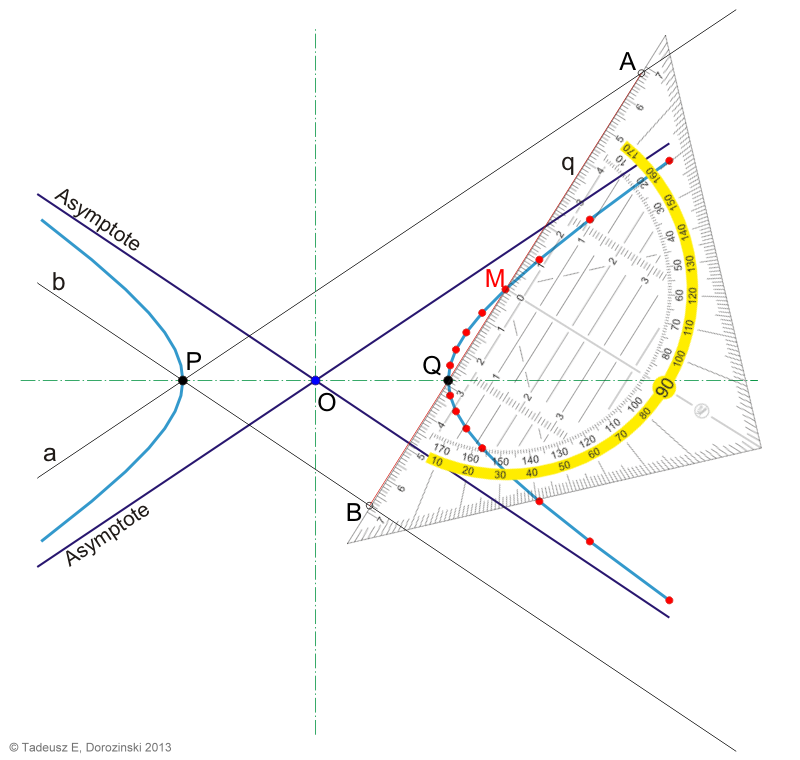
Unten sehen wir die neue Bestimmungsmethode der Punkte, die auf dieser Hyperbel liegen mit Hife eines Geodreiecks.

Zuerst zeichnen wir zwei Geraden a und b durch den punkt P, parallel zu beiden Asymptoten. Ein Geodreieck wir so angelegt, dass seine Hypotenuse durch den Punkt Q verläuft. Dabei achten wir darauf, dass die Schnittpunkte der Hypotenuse mit den Geraden a und b  in gleichem Abstand vom Nullpunkt des Massstabs auf dem Geodreieck sich befinden. Wir markieren diesen Punkt (in der Zeichnung als M bezeichnet). Dieser Punkt liegt auf der Hyperbel. In gleicher Weise markieren wir weitere Punkte, was uns erlaubt die Hyperbel zu zeichnen.

Im Falle, dass nur die beide Asymptoten und ein beliebiger Punkt einer Hyperbel gegeben sei, können wir zuerst die beide Scheitelpunkte konstruiren.

Datei zum Downloaden:     GeoGegra-Datei (GGB-Format)

© Tadeusz E. Dorozinski

Stand: 23.04.2013