Goldene Ellipse

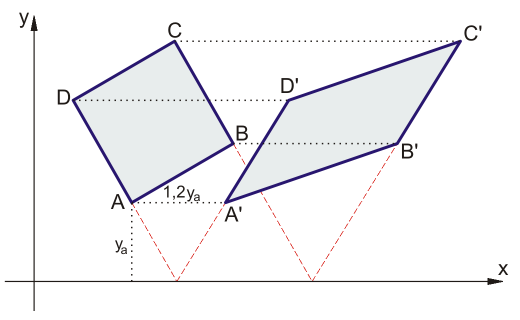
Einige Transformationen der Ebene verformen ein Kreis zu einer Ellipse.

Zu diesen Transformationen gehört auch die Scherung (Transvektion).

Zu Errinerung: bei Scherung jedem Punkt der Ebene P(x,y) entspricht der punkt P(x',y'), dabei  x' = x + k y  und  y' = y.
Der Parameter k ist eine beliebige Zahl, jedoch k ≠ 0. 
Unten ein Beispiel für k = 1,2. 

Dr. Bronek Pabich hat im Jahre 2008 rausgefunden, dass für k = 1 ein Kreis in eine Ellipse umgeformt wird, wo die Goldene Zahlen dreimal vorkommen!
Er hat das in der polnischen Zeitschrift "NiM + Ti", im Heft 66/2008 publiziert.

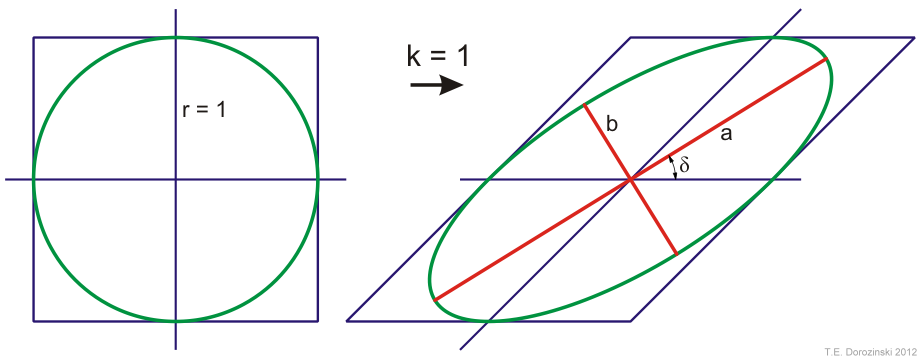
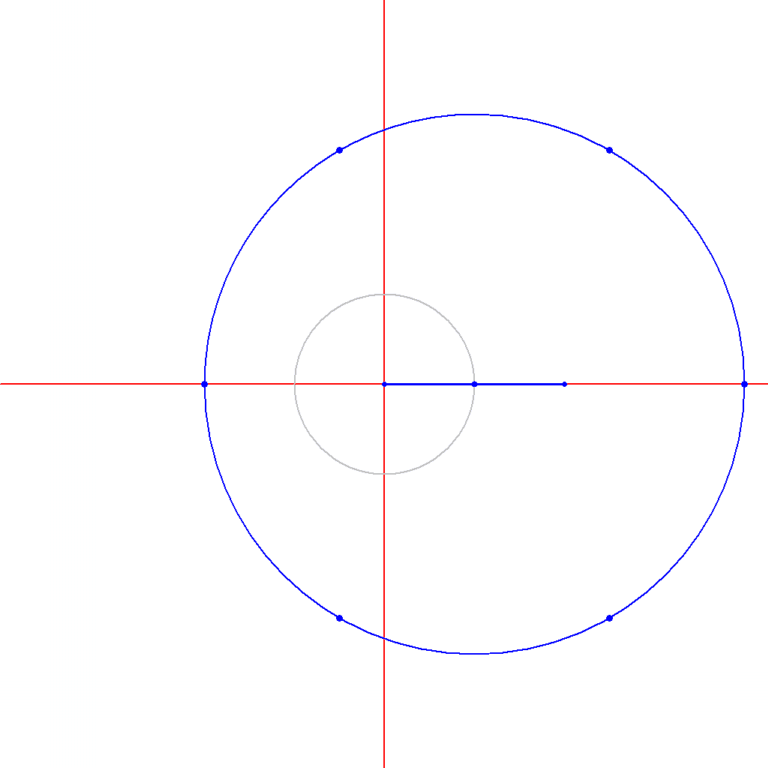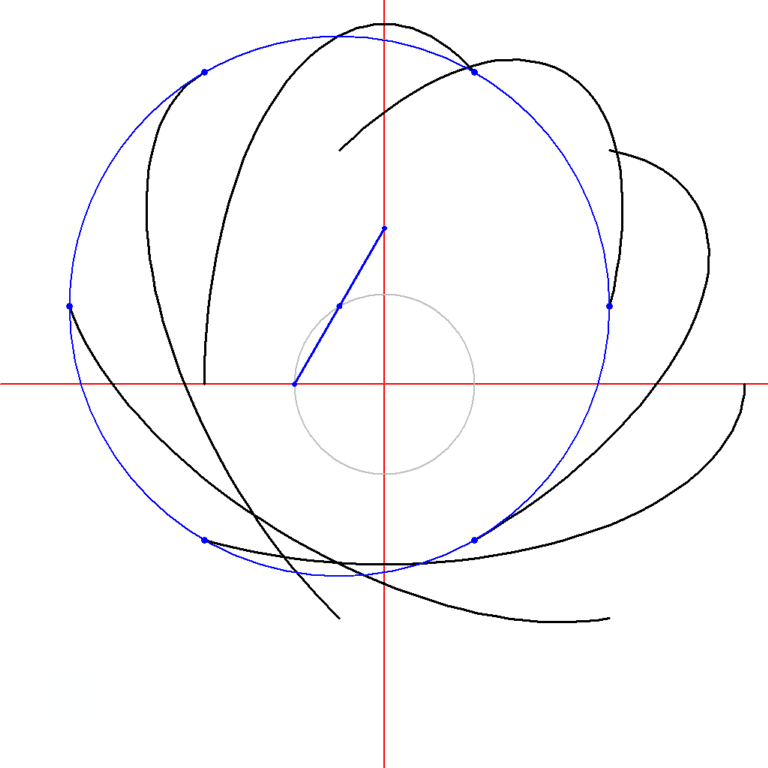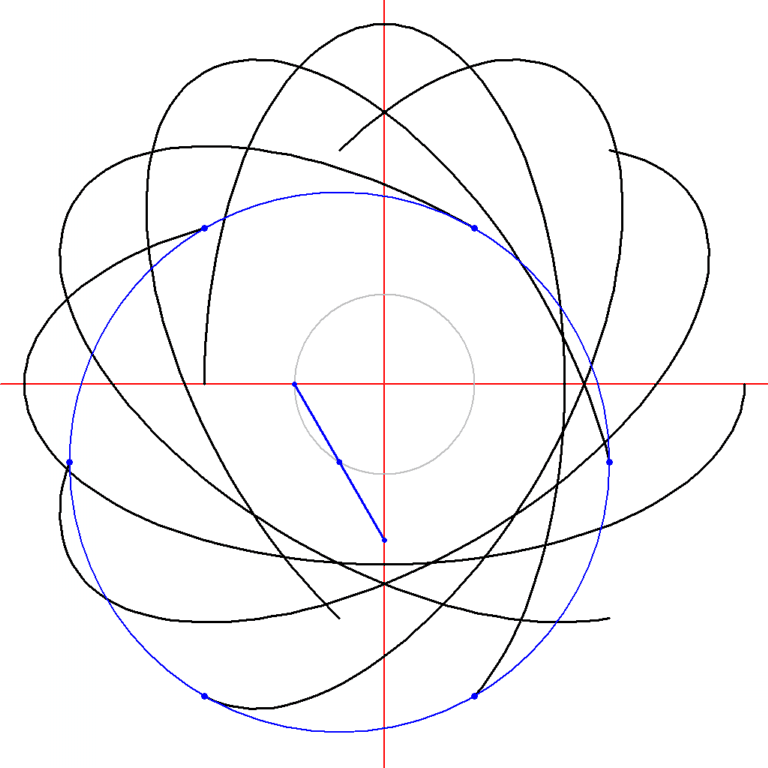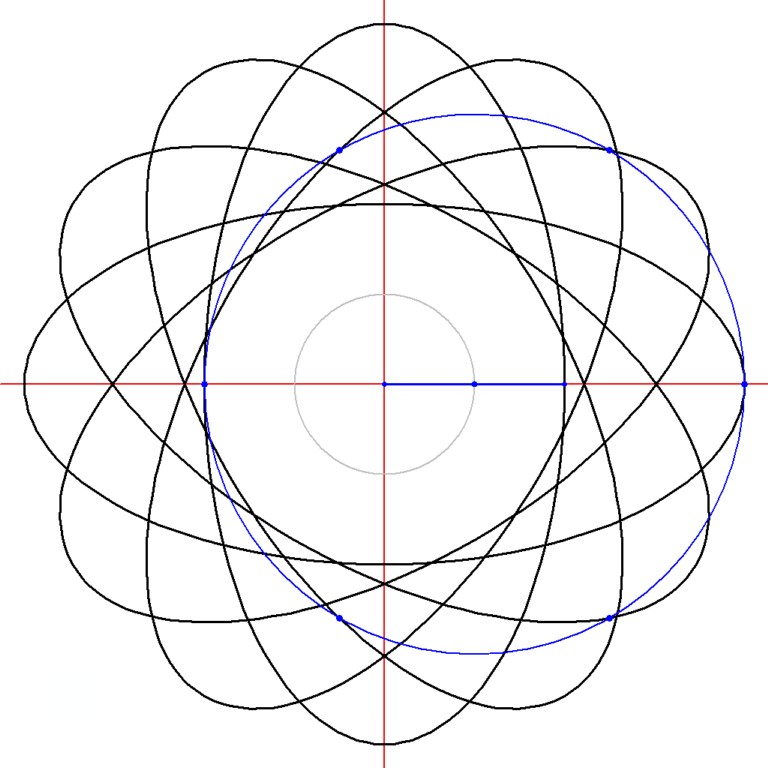
Die beide Halbachsen haben Längen der großen und kleinen Goldener Zahl. Auch die Neigung der großen Achse (Winkel δ) hat etwas mit der Goldener Zahl zu tun.

Da haben wir entsprechend:  a = Φ =1,618,  b = φ = 0,618 und  tan δ = 0,618.

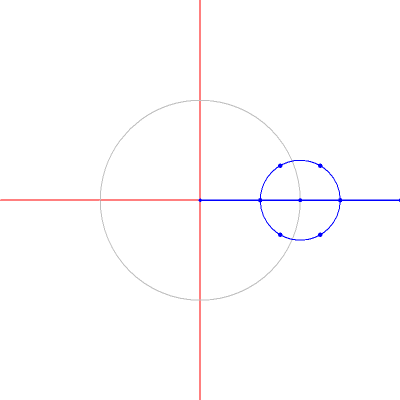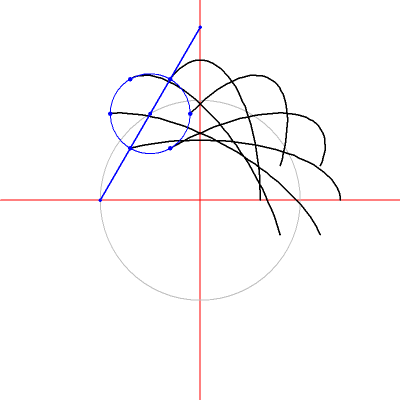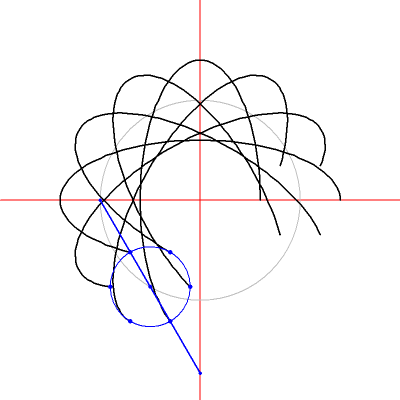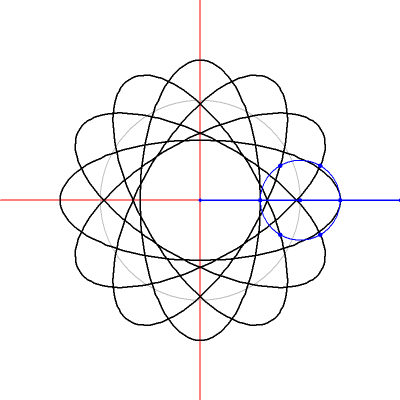
Scherung der Parabel

Interessant ist der Fall der Parabel. Durch die Scherung einer Parabel erhalten wir die gleiche (kongruente) Parabel. Nur ihre Achse ist verschoben.

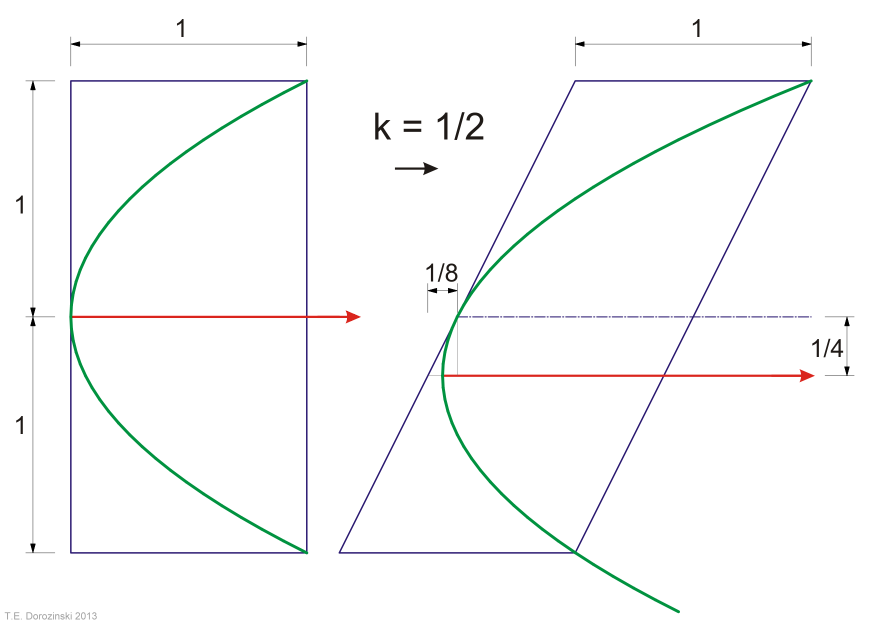
Im Beispiel oben ist k = 1/2. Die Parabelachse ist um 1/4 verschoben (warum?) 

© Tadeusz E. Dorozinski
im August 2012 / Januar 2013

E-Mail:
info@3doro.de