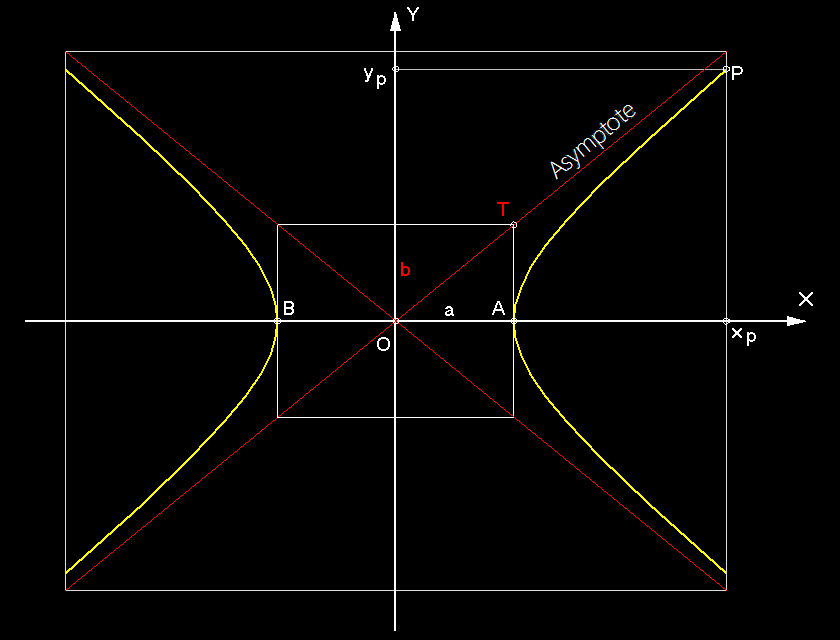
Hyperbel

Bestimmung der Asymptoten

Vorgegebene Elemente:

1. Die große Achse AB mit der Länge 2a
2. Beliebiger Punkt P auf der Hyperbel, deren Koordinaten  sind: x_p und y_p

_{Um die Lage der Asymptoten zu bestimmen, genügt es die Länge b der kleinen, imaginären Halbachse zu ermitteln.
Die errechnen wir aus der Formel:}

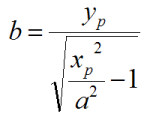
_{Die erste Asymptote geht durch den Mittelpunkt O und durch den Punkt T(a,b). Die zweite Asymptote ist spiegelbildlich zu erster, bezüglich der Achse X.}

_{* * *}

_{Man kann das auch konstruktiv machen. Siehe hier: PDF-Datei}

Aufgabe

_{Gegeben sind beide Asymptoten einer Hyperbel und ihr beliebiger Punkt P (wie unten dargestellt).}

_{Man bestimme konstruktiv den Scheitelpunkt A der Hyperbel, der sich auf der waagerechten Achse befindet.}

© Tadeusz E. Dorozinski, 2007, 2011, 2018

E-Mail:
info@3doro.de