Kegelschnitte als Projektion der Durchdringungslinien von zwei Quadriken

In einigen speziellen Fällen kann die Durchdringungslinie von zwei Quadriken als eine Ellipse, eine Parabel bzw. eine Hyperbel in der Ansicht (bei normaler Projektion) erscheinen.

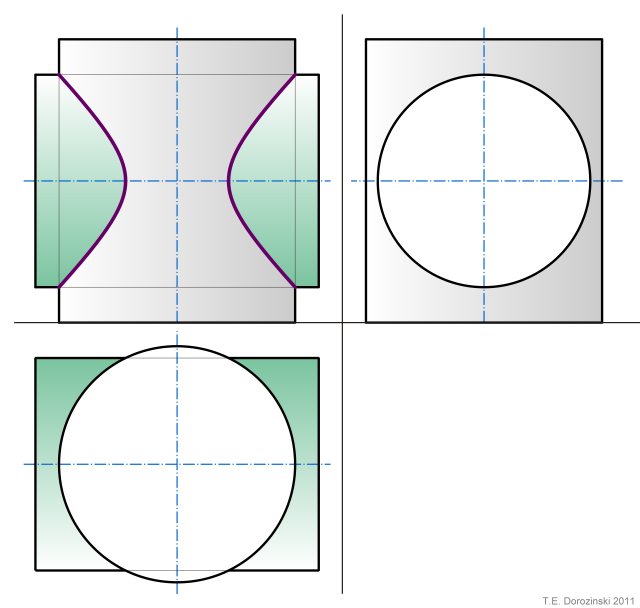
1. Hyperbel

1.1  Zylinder - Zylinder

1.2  Kegel - Zylinder (schräge Achse)

1.3  Kegel - Zylinder (waagerechte Achse)

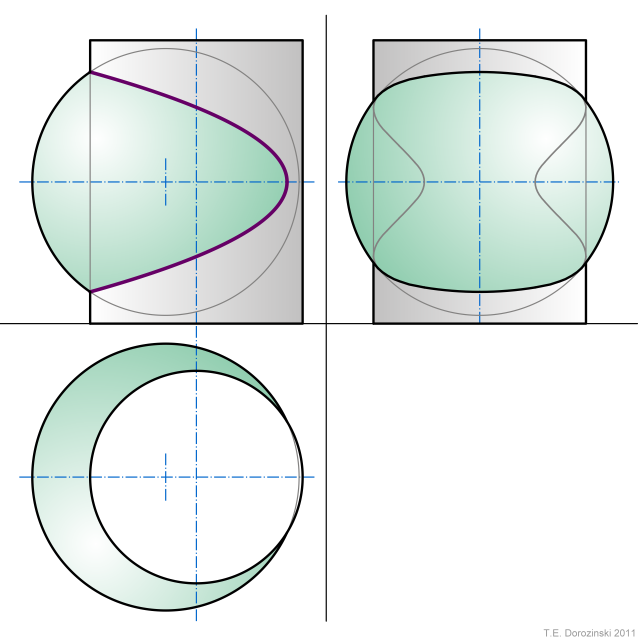
2. Parabel

Kugel - Zylinder

* * *

Kugel - Kegel 
Kugel berührt eine einzige Erzeugende des Kegels in einem Punkt.
Konstruktion im Aufriss beliebigen Punkte der Parabel zeigt diese Zeichnung.

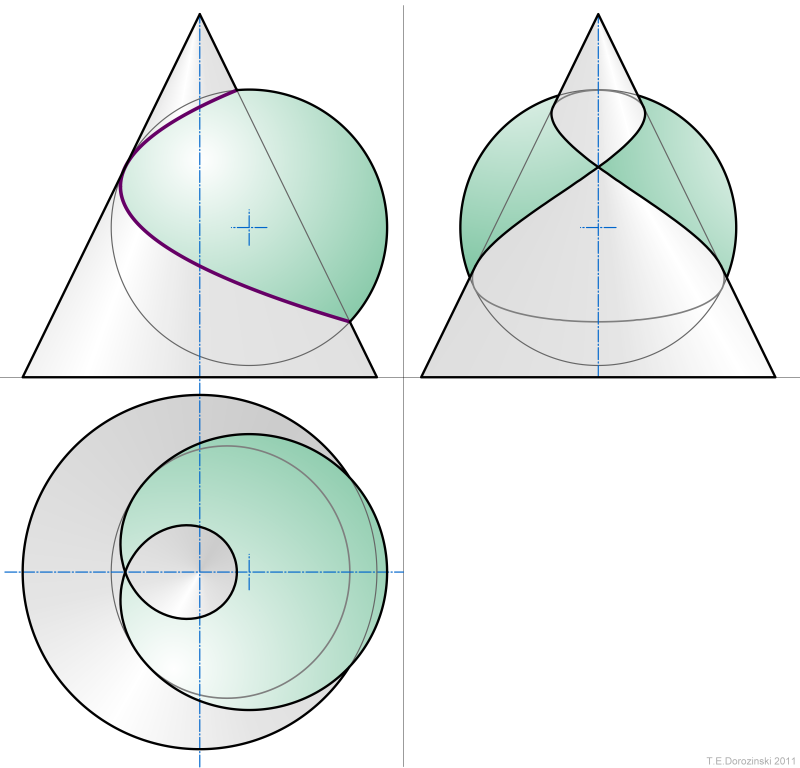
3. Ellipse

Kugel - elliptischer Kegel

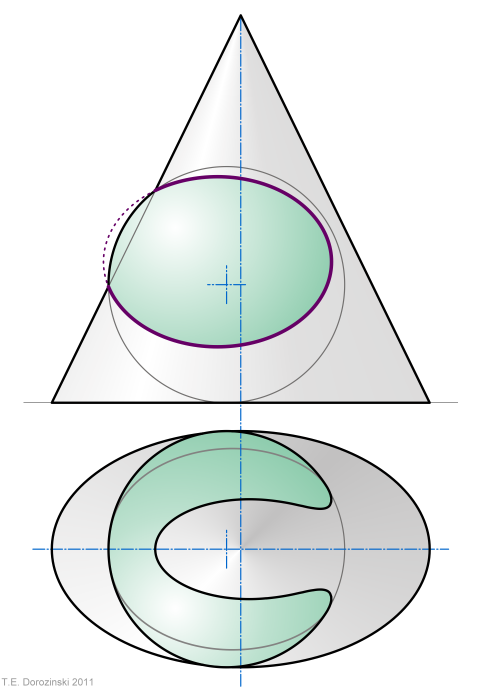
Einschaliges Hiperboloid - Zylinder
Wir sehen die Durchdringungslinie in der Draufsicht als Ellipse und in der Vorderansicht als Hyperbel.

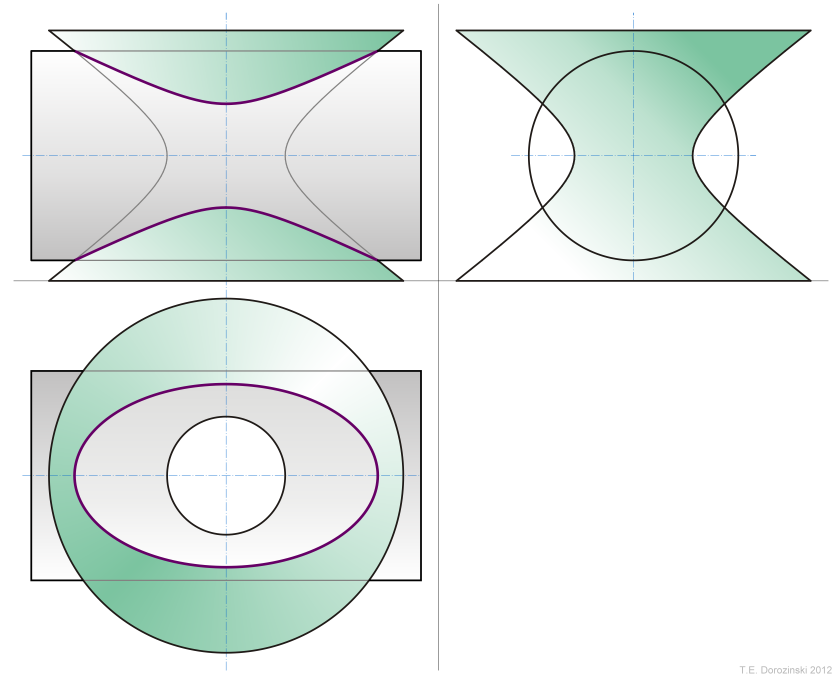
Die Durchdringungslinie ist also die gemeinsame Kurve für 4 Quadriken: einschaliges Hyperboloid, Kreiszylider, elliptische und hyperbelische Zylinder.  Hier als o2c-Objekt.

Noch die fünfte Quadrik kann man durch diese Kurve durchführen, und zwar ein elliptischer Kegel.

© Tadeusz E. Dorozinski

Stand: 24.01.2013