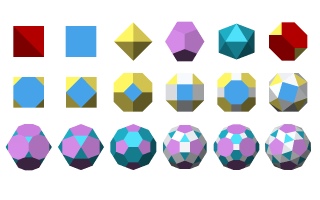
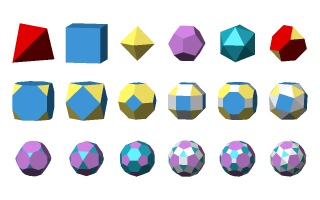
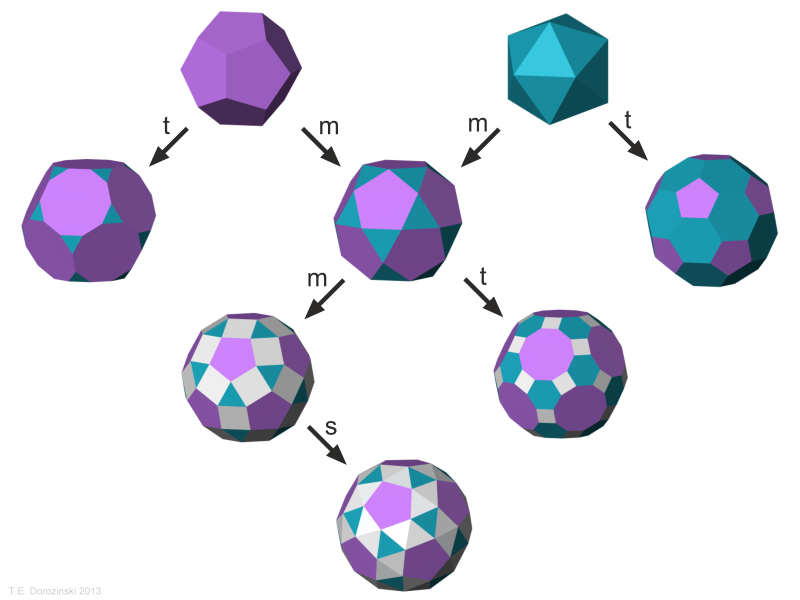
Operationen an regulären Polyedern
Es gibt drei Operationen, die ein reguläres Polyeder modifizieren:
Abstumpfung (Ecken abschneiden) - bezeichnet mit t (von eng. truncation),
Mittelpunkt-Abstumpfung - bezeichnet mit m (von eng. midpoint). In Englisch wird sie auch als ambo oder rectification bezeichnet.
Verdrehung - bezeichnet mit s (von eng. snub bzw. lat. simus).
So kann mann aus den fünf platonischen Körpern die 13 archimedischen Polyeder erzeugen.
Notabene, diese drei Operationen kann man auch an anderen regulären Figuren anwenden, z. B. an 2D und 3D-Netzen.
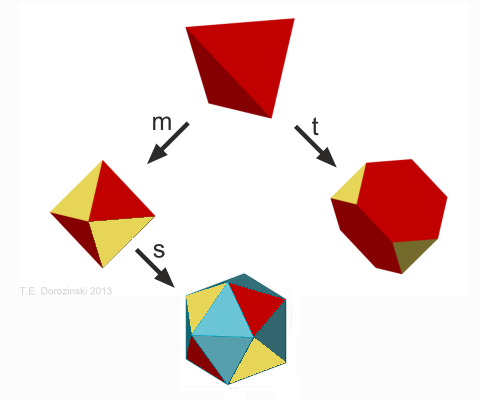
Bemerkung
Von fünf platonischen
Körpern nur drei sind primitiv, simpel - Tetrauder, Kubus und Dodekaeder. Oktaeder und Ikosaeder enstehen durch
entsprechende Operationen am Tetraeder.
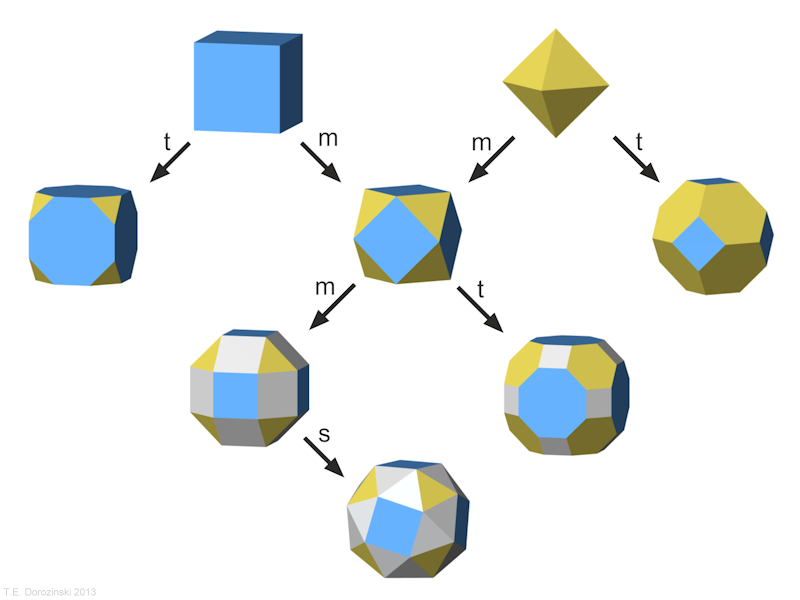
Die Operationen m und t an archimedischen Polyedern.
'Snub'-Operation (nach H.S.M. Coxeter)

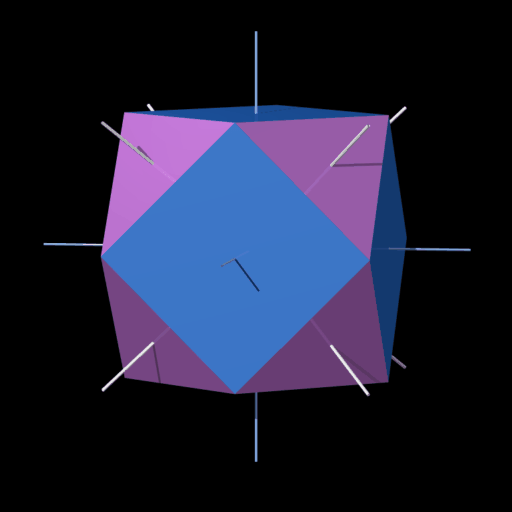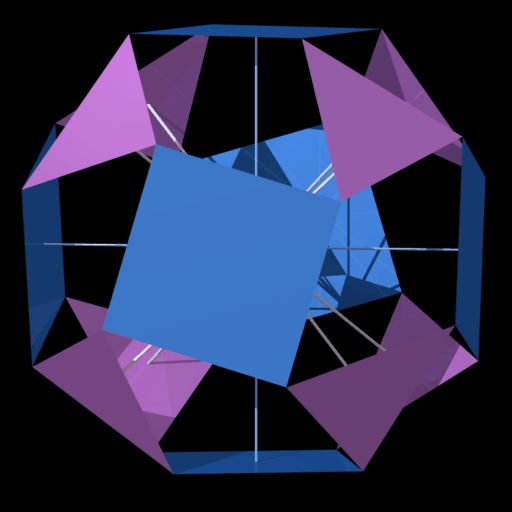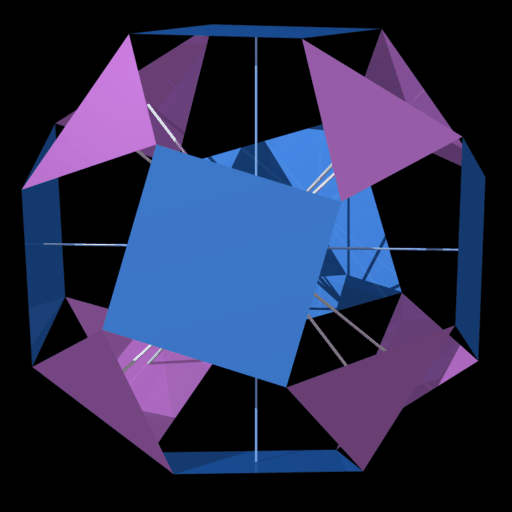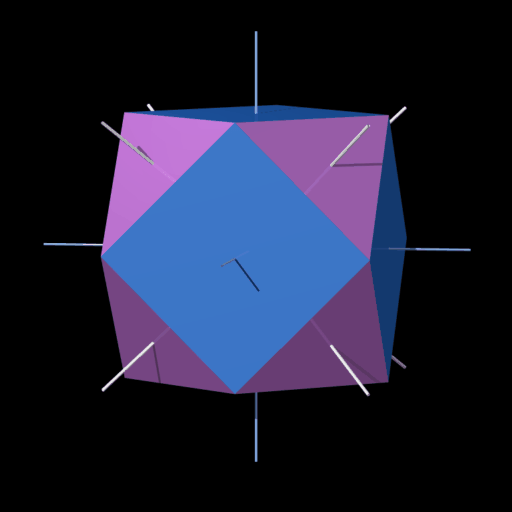
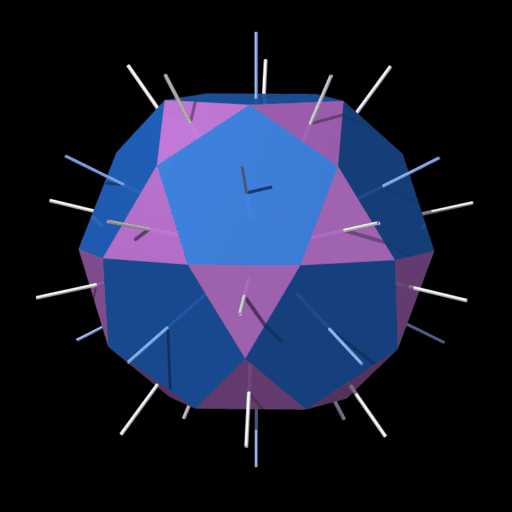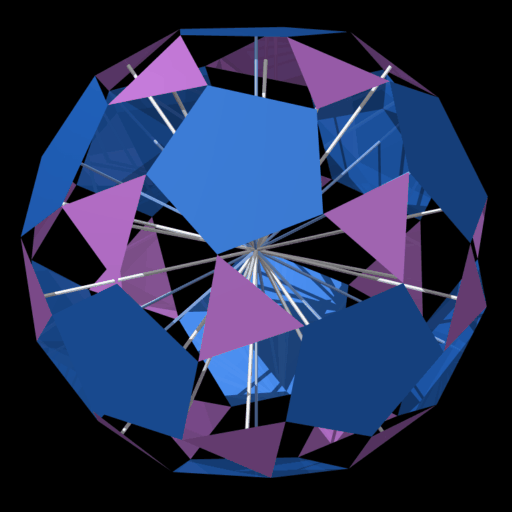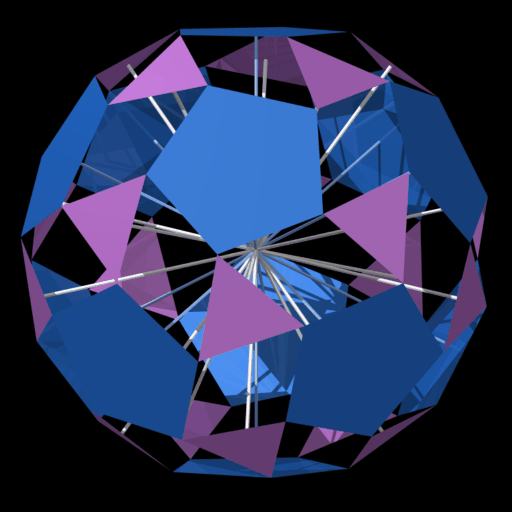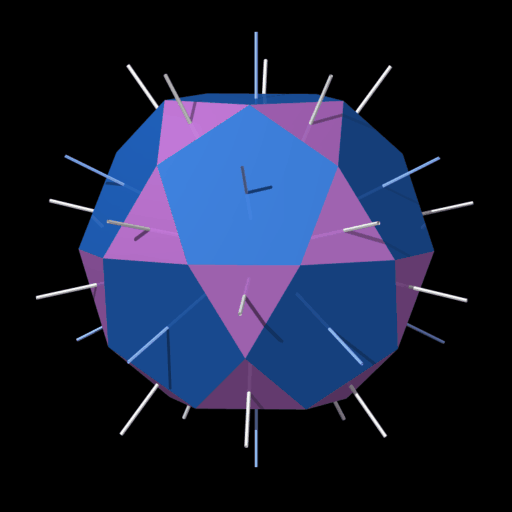
Andere Verdrehungen

Durch die Operation s am
Rhombenkuboktaeder (A5) entsteht ein abgeschrägtes Hexaeder (A7, cubus simus).
Die Quadrate werden um
16,4675° und die Dreiecke um -20,315° verdreht.
Die 24
Ebenen der weißen Dreiecken, die nach der Drehung entstehen, bilden ein 24-Flächner (Pentagonikositetraeder),
der aus gleichen Fünfecken zusammengesetzt ist.
Die Umwandlung des Rhombenkuboktaeders in ein abgeschrägtes Hexaeder kann man in Stella4D realisieren. Hier wird es gezeigt wie.
* * *

Durch die Operation s am
Rhombenikosidedekaeder (A11) entsteht ein abgeschrägtes Dodekaeder (A13, dodecaedron
simum).
Die Fünfecken werden um 13,1064°
und die Dreiecke um -19,518° verdreht.
Analog entsteht ein 60-Flächner (Pentagonhexakontaeder).
Ein Polyeder mit der Symmetrie des Tetraeders, dessen sämtliche Seitenflächen irreguläre Fünfecken sind, ist bekannt unter dem Namen: Tetartoid oder tetraedrisches Pentagondodekaeder.
* * *
Zwei verdrehte archimedische
Polyeder. Die Verdrehung wurde von Eduard
Baumann ermittelt.
STEL-1, STEL-2


* * *
Andere Transformationen
Expansion






Einige Polyeder kann man partiell expandieren. Unten ein Beispiel.
Das tetraedrisch expandierte Rhombendodekaeder ist ein 28-Flächner mit der Symmetrie des Tetraeders:
Ein anderer 28-Flächner hat Enrico Bernal gefunden:
Verwandt mit dem 28-Flächner ist dieses Polyeder:
und hier ein voll expandiertes Rhombendodekaeder:
Die drei oben dargestellte Polyeder lassen sich umwickeln.
Transformationen platonischen Körper
* * *
Expansion mit Verdrehung (engl. Twirl )


Unten ein Beispiel für partielles Expandieren mit Verdrehung.
Jitterbug

Bizarre Verdrehung




Expansion spezial
Zwei modifizierte archimedische Polyeder (near missis Johnson Solids).
Ein 182-Flächner und seine duale Form:
und ein 242-Flächner und seine duale Form:
© Tadeusz E. Dorozinski
Erstellt: 25.07.2008
Stand: 29.03.2024