Hier ein Beispiel der Konstruktion
einer Kuppel des Typs m,
n=0 (Klasse I).
Die Kuppeln mit der Frequenz m<7 kann man relativ leicht mit den Methoden der
darstellenden Geometrie konstruieren.
Ab m=7 ist es am besten so vorzugehen:
Als
Ausgangsform fungiert das Ikosaeder.
Es genügt nur ein Segment zu konstruieren, da die anderen gleich sind.
Auf einer Seite des Ikosaeders wird ein Kugeldreieck ABC gebildet, das auf der Oberfläche einer Kugel mit dem Mittelpunkt O liegt (Abb. 1)
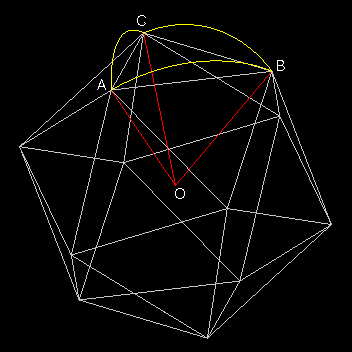
Abb.1
Die drei Bögen AB, BC und AC
werden in m gleiche Teile
untergeteilt (Methode II). In unserem Beispiel ist m = 7
(Abb.
2)
Hinweis: nach der Methode I wird das Dreieck
ABC in kleine, gleiche Dreiecke untergeteilt und deren Eckpunkte werden auf
die Kugeloberfläche projiziert.
Die Methode I ist einfacher als die Methode II, liefert aber mehr
unterschiedlichen Kantenlängen.
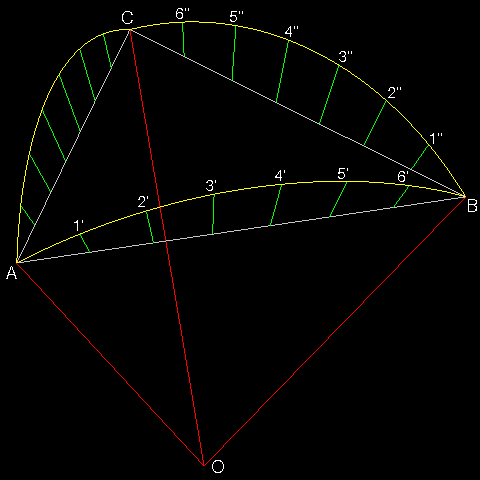
Abb.2
Durch die Punktepaare 1'-6'',
2'-5'' usw. zeichnen wir die Großkreise mit dem Mittelpunkt O.
Die Bögen innerhalb des Kugeldreiecks ABC bilden ein Netz (Abb. 3,
gelb)
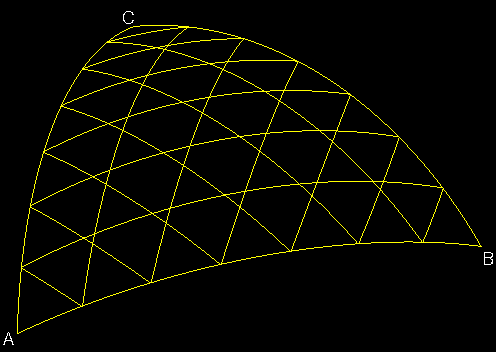Mauscursor auf das Bild = Segment optimiert
Abb. 3 und 4
Jeweils drei Bögen bilden innerhalb
des Kugeldreiecks ABC keine richtige Knotenpunkte, sondern kleine
Kugeldreiecke.
Die Mittelpunkte diesen Dreiecken sind die gesuchten Ecken unseren Segments
(Abb. 4, weiß).
Die oben beschriebene
Operationen kann am besten mit Hilfe des Computers durchführen.
Ich mache es mit einem kleinen Basic-Programm.
Abb. 5 zeigt das Prinzip der
Methode I, wobei hier m = 4.
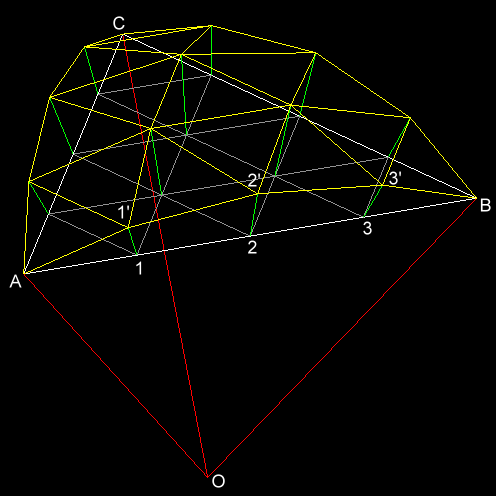
Abb. 5
Das Dreieck ABC ist in 16 kleinen, gleichseitigen Dreiecken aufgeteilt, deren Eckpunkte auf die Kugeloberfläche projiziert werden.
*****
Die Dreiecke im Segment sind natürlich nicht alle gleich. Da so ein Segment
symmetrisch aufgebaut ist, kommen einige Dreiecke dreimal, andere sechsmal
vor.
Wenn m
eine Zahl vom Typ 3i-1
ist, wobei i = 0, 1, 2
..., dann in der Mitte
des Segments befindet sich ein einziges gleichseitiges Dreieck.
Je größer m
ist, desto
größer ist die Anzahl der Dreieckstypen, die wir mit t
bezeichnen.
Für die Kuppeln der Klasse I kann die Anzahl der Dreieckstypen t (abhängig vom m) nach folgenden zwei Formeln berechnet werden:
Wenn m durch 3 teilbar ist, dann:
(1) t(m) = m *(m + 3) / 6
sonst:
(2) t(m) = (m + 1)*(m + 2) / 6
Für die Kuppeln der Klasse II, wo m = n kann die Anzahl der Dreieckstypen t (abhängig vom n) nach folgender Formel berechnet werden:
(3) t(n) = n *(n + 1) / 2
*****
Kuppeln der Klasse I und
II nach der Methode I kann man relativ einfach im Programm Stella4D
bzw. GreatStella erzeugen. Auch Kuppeln der Klasse III im Falle n = 2m.
Die Kuppeln der Klasse I kann
man nach einfacheren Methode I oder komplizierteren Methode II
(siehe oben) erzeugen.
Die Resultate der beiden Methoden sind nicht gleich. Frage ist: welche
Methode liefert gleichmäßigere Unterteilung in Dreiecke?
Die Antwort bekommt man, wenn man die vergleicht.
Vergleich der Methode I und II
Literatur:
1. Hugh Kenner
Geodesic
Math and How to Use It University of California Press, Berkeley
1976
2. Magnus J. Wenninger Spherical Models Dover
Publications, New York 1979
3. Jacek Fulinski Geometria kratownic powierzchniowych
Prace Wrocławskiego
Towarzystwa Naukowego, Wrocław
1973
4. Jacek Fulinski, Tadeusz Kolendowicz Kształtowanie
geometryczne niektórych kopuł
geodezyjnych Zeszyty
naukowe Politechniki Wrocławskiej
1973
Links:
Wikipedia
deutsch
Wikipedia
englisch
Wikipedia
französisch
Tutorial
von Jürgen Meier
© Tadeusz E. Dorozinski
Stand: 26.07.2018