Reguläre und halbreguläre 3D-Netze (Raumgitter)

in Arbeit

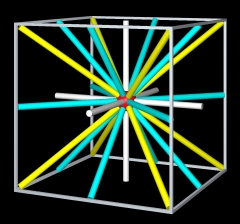
Die Grundfigur der regulären Netze ist der Kubus (Würfel).
Vom Mittelpunkt des Würfels (Netzknotenpunkt) führen 6 Strahlen (Bindungen) zu Mittelpunkten der Flächen,
8 zu Ecken  und 12 zu Mittelpunkten der Kanten.

Aus diesen Elementen werden reguläre  3D-Netze ( engl. 3D Nets  or 3D Lattice) gebaut.
"Die Regularität" bedeutet hier das, dass die 3D-Netze drei gleichwertige Translationen in drei senkrecht zueinander Richtungen aufweisen.
Interessant sind auch deren Unternetze (Untergitter) und deren Modifizierungen und Kombinationen. 

Alle Netzknotenpunkte von solchen Netzen bilden reguläre und halbreguläre Punktgitter.

Oft die benachbarte Bindungen der 3D-Netze liegen auf einer Gerade.  Solche Netze werden  'Geradennetze' genannt.

Die Eckpunkte und Kanten von Raumfüllern (Polyeder die lückenlos den Raum füllen) bilden oft reguläre und halbreguläre 3D-Netze.

Mögliche Bindungen:

Bemerkung
Durch alle Bindungen verlaufen Drehachsen: 2- bzw. 4-zählige durch die weiße, 3-zählige durch die gelbe und 2-zählige Drehachsen durch die grünblaue Bindungen.

6-Netze:

Kombination 6+4

8-Netze:

Zwei Kombinationen 4+8

1. Kombination

2. Kombination

Kombination 6+8

12-Netze:

Kombination 12+4p

Kombination  6+4p

Kombination  6p+4p

Kombination  12+12-6p

Kombination  12-4-2+12-4

Modifizierte Netze:

Folgende Begriffe sind mit den  regulären Netzen verbunden:

1. Dual-Netze (engl. interwoven nets). Man spricht von der Interpenetration der 3D-Netze, oder dass zwei 3D-Netze verflochten sind.
2. Eckfigur (engl. Vertex Figure)
3. Dirichlet-Voronoi-Zelle* (Polyeder, DV-Zelle, engl. DV-Cell)
4. Bindungszelle** (Polyeder, BZ, engl. CC = Conection Cell)

Alle drei beschreiben gut die Eigenschaften vom jeden regulären Netz.

* Dirichlet-Voronoi-Polyeder (engl. DV cell) beinhaltet alle Punkte, die einem Knotenpunkt näher liegen als irgendwelchen andere Knotenpunkt des Netzes. Es wird auch als 'Wirkungsbereich des Knotenpunkts' bezeichnet.

** Bindungszelle beinhaltet alle Punkte, die einer Bindung näher liegen als irgendwelchen anderer Bindung. Es wird auch als 'Wirkungsbereich der Bindung' bezeichnet.

Alle DV-Zellen und alle Bindungszellen sind Raumfüller.

Die Anzahl und die Lage der Bindungen bestimmen die Dichte der regulären Netze und die kann man als eine Zahl ausdrücken.
Die Dichte d  wird als der Quotient der Längensumme aller Bindungen, die sich im Fundamentalbereich befinden, dividiert durch den Volumen des Fundamentalbereichs, wobei  eine Bindung die Länge = 1 hat.

So z. B. hat das Netz 6 die Dichte d = 3. Drei Bindungen in einem Kubus, dessen Kante gleichlang wie eine Bindung ist.

Alle Knotenpunkte bilden immer ein Punktgitter, das auch als reguläres Punktsystem genannt wird. 
Die Dichte δ eines Punktgitters ist umgekehrt proportional zum Volumen seines Dirichlet-Voronoi-Polyeders, wobei der Abstand zwei benachbarten Punkten 1 beträgt.

Startseite