n12-3

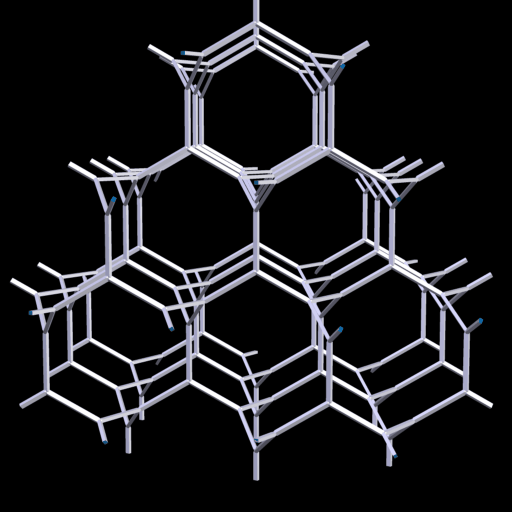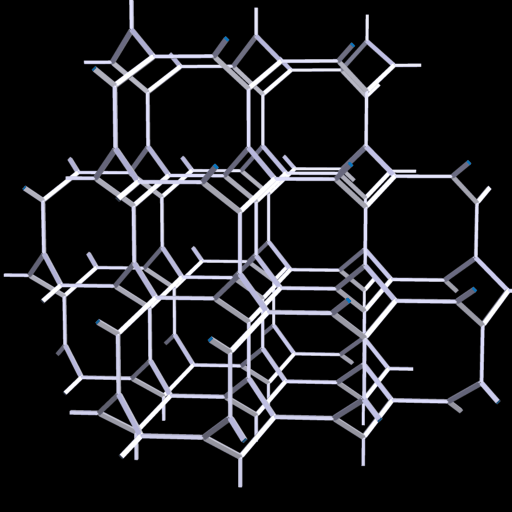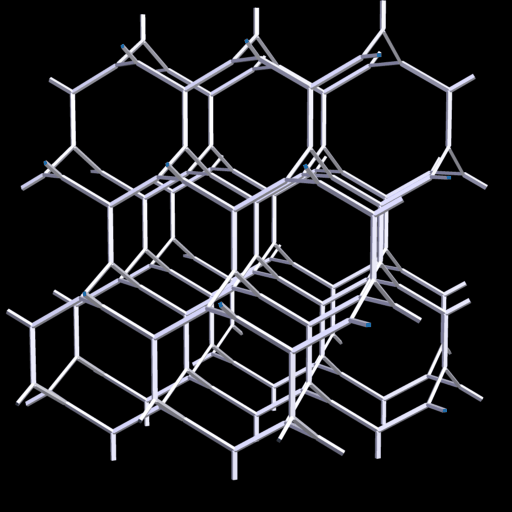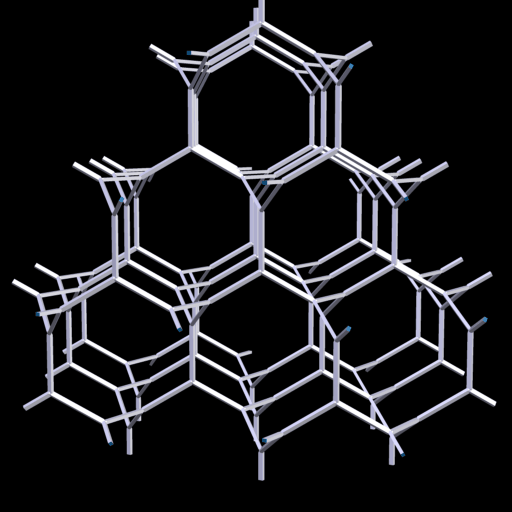
H.S.M. Coxeter nannte dieses 3D-Netz  'the Laves graph' und A.F. Wells als 'The Uniform Net (10,3)'.

Netz 12-3

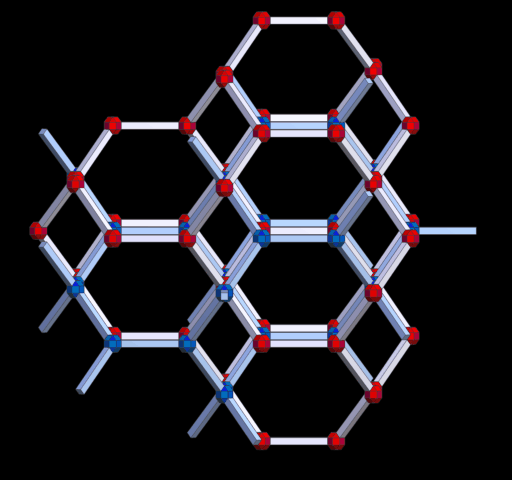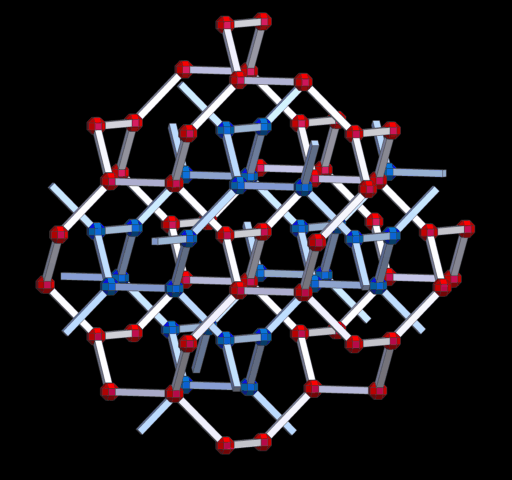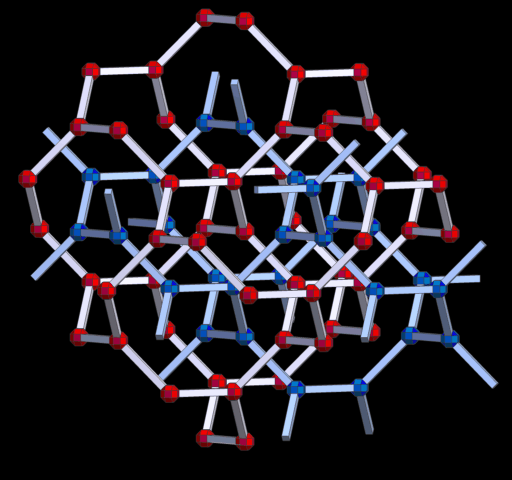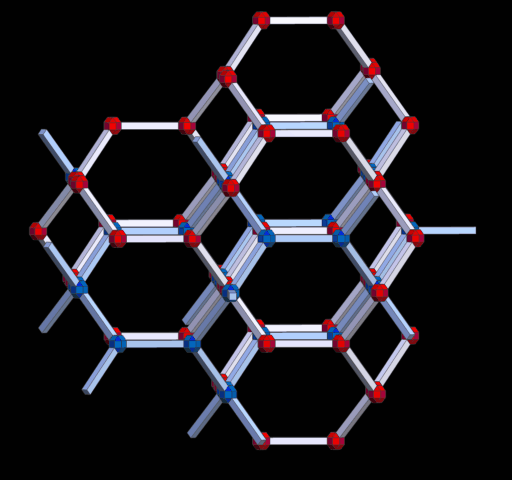
Netzdichte: d = 0,5303
Die Dichte des Punktgitters: δ = 0,3535
Die Eckfigur ist ein regelmäßiges Dreieck.
Die Dirichlet-Voronoi-Zelle von diesem Netz ist relativ kompliziert. Es ist ein Polyeder mi17 Flächen (siehe Bild unten).

Die Oberfläche besteht aus 3 Achtecken, 2 Sechsecken, 6 Fünfecken und 6 Vierecken.

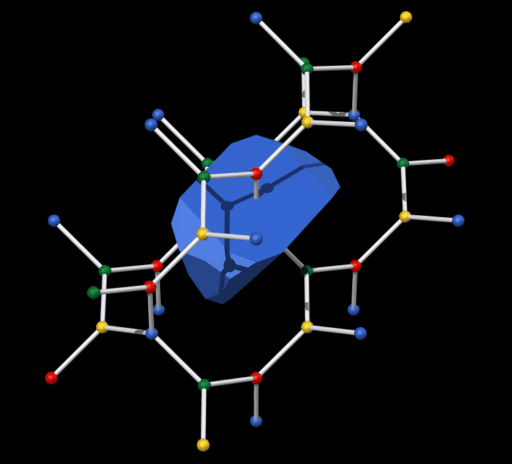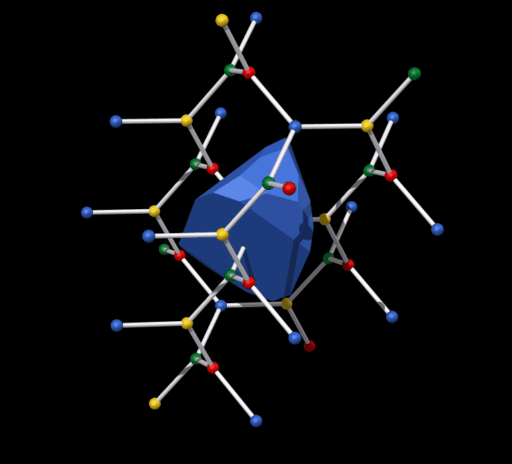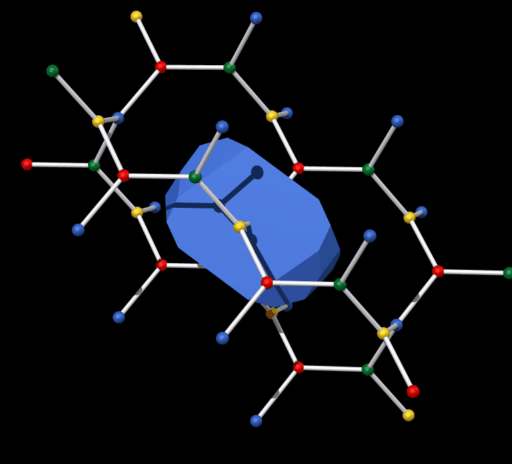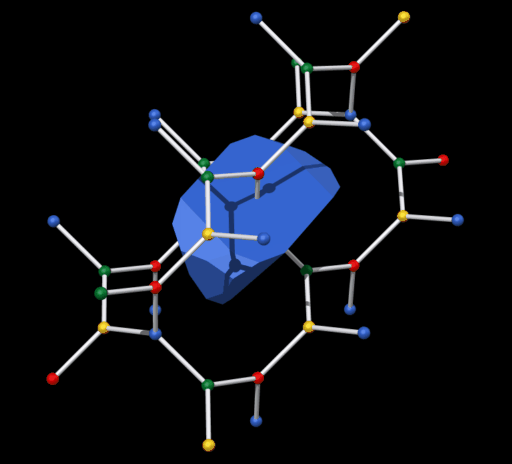
Mit diesem Polyeder kann man der Raum lückenlos füllen (parkettieren).
Es ist ein Plesiohedron. OFF-Datei
Unten die kleine Animation, die dieses Polyeder als Raumfüller zeigt:

Die Bindungszelle (CC) ist ein Zwölfflächner (zwei chirale Formen).

   OFF-Datei

Bindungen "bilden" kleine Zellen. So eine Zelle kann man ale ein nicht konvexes Polyeder darstellen.

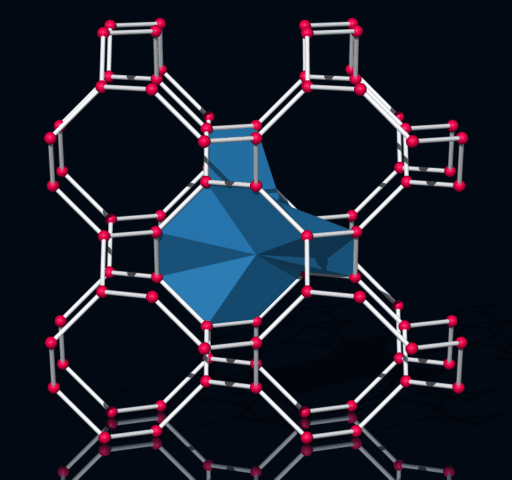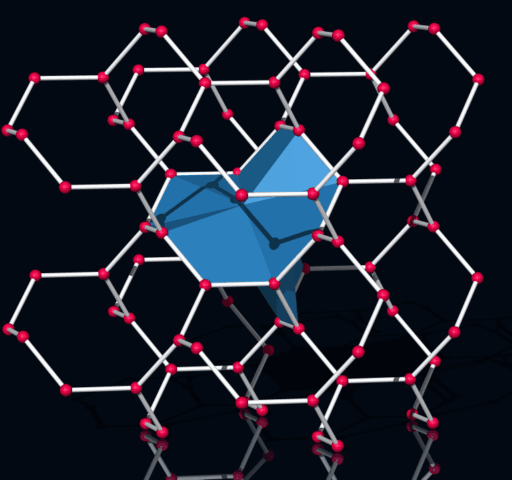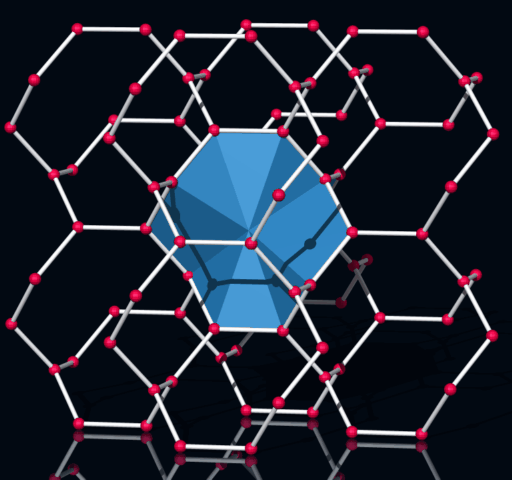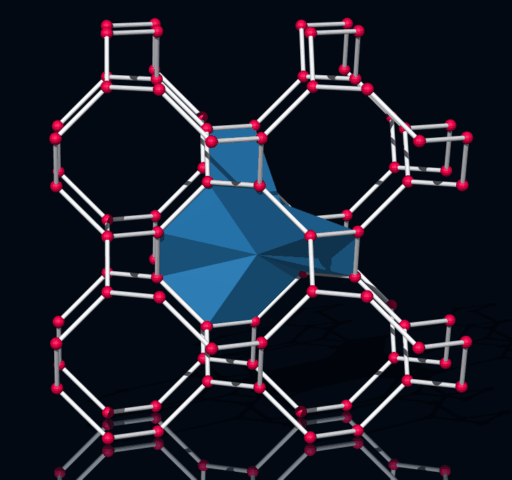
So ein Polyeder hat 24 Flächen und eine dreifache Rotationsachse.

Es ist der dritte Raumfüller, der vom Laves-Graph abgeleitet wird. Auch seine Koordinaten der Eckpunkten sind ganzzahlig (Integer).  OFF-Datei
Unten ein Ausschnitt  der Raumfüllung, die keine Symmetrieebenen hat.

.