Parkettierungen

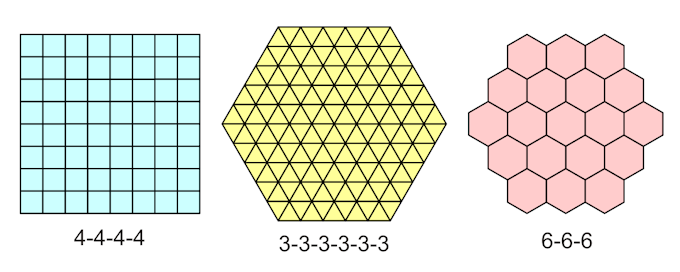
Reguläre und halbreguläre Parkettierungen

(engl. regular and semiregular tilings)

Bekannt und oft beschrieben sind reguläre (platonische) und halbreguläre (semireguläre oder archimedische) Parkettierungen.
Sie sind aus regelmäßigen Dreiecken, Vierecken, Sechsecken, Achtecken und Zwölfecken gebaut. Alle Ecken (Knotenpunkte) sind gleich.

Unten drei platonische Parkettierungen

und da unten sieben archimedische Parkettierungen.

Die zwei letzte Parkettierungen haben zwei gespiegelte Formen.

Vier Parkettierungen haben 3-fache Knotenpunkte, drei - 4-fache, zwei - 5fache und eine hat 6-fache Knotenpunkte.

Expandierte Parkettierungen

Die mittlere Zahl der Nachbarn

Eine Parkettierung der Ebene kann man als Landkarte mit unendlich vielen Länder (Vielecken) betrachten, dabei fungieren Kanten als Grenzen.
Eulersche Formel gilt für Landkarten, also auch für Parkettierungen. Also haben wir

E + F - K = 2 (1).

wo E die Anzahl der Ecken (Knotenpunkte), F die Anzahl der Flächen und K die Anzahl der Kanten ist.

Bezeichnen wir mit N die mittlere Zahl der Nachbarländer einer Landkarte. Natürlich ist

N = 2K / F (2).

Es ist offensichtlich, dass für drei reguläre Parkettierungen die Zahl N entsprechend 3, 4 und 6 ist.
Wie sieht es mit der Zahl N für halbreguläre Parkettierungen? Die Antwort ist ein wenig komplizierter.

Bezeichnen wir mit v die Vielfachkeit der Knotenpunkte. Für halbreguläre Parkettierungen v beträgt 3, 4 und 5.

Berechnen wir N(v) für v = 5.

In diesem Fall haben wir

5E = 2K (3).

Aus (1) und (3) erhalten wir

3K = 5F - 10

und folglich

N(5) = 10/3 - 20/3F

Da für Parkettierungen F unendlich groß ist, erhalten wir

N(5) = 10/3 = 3,(3)

Analog

N(3) = 6 und N(4) = 4

* * *

Konvexe Siebenecke und die mittlere Zahl der Nachbarn

Parkettierungen aus Parkettierungen

Man kann einige benachbarte Vielecke einer archimedischen Parkettierung so gruppieren, dass ein Cluster (ein Prototile) entsteht, mit dem man die ganze Ebene überdecken kann. Wir erhalten also eine neue Parkettierung.

Nehmen wir beispielweise die Parkettierung 4-8-8. Wir verbinden ein Achteck mit einem benachbarten Quadrat.

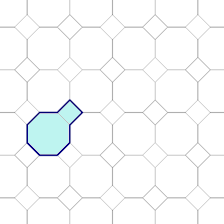
Mit dem entstandenen Zehneck kann man die ganze Ebene überdecken.

Es ist nicht die einzige Lösung. Durch das Drehen des Prototiles erhalten wir andere Mustern.

Man kann auch mehrere Achtecke und Quadrate verbinden. Es ist wichtig dabei, dass die Anzahl der Kanten von allen gewählten Vielecken durch N(v) teilbar ist (warum?).
In unserem Fall die Anzahl der Kanten beträgt 8 + 4 = 12 und N(3) = 6.

Interessant sind vor allem die kleinsten Prototiles der archimedischen Parkettierungen.
Wie sieht es so ein Prototile der Parkettierung 3-3-3-3-3-6 aus?

Auch aperiodische Parkettierungen möglich sind:

Stand: 21.08.2016

Kontakt