
Konvexe
Siebenecke
und die Mittlere Zahl der Nachbarn.
Paradox?
M.
Gardner und H. Steinhaus (Mathematical Snapshots) haben eine nicht reguläre Bedeckung der Ebene mit konvexen Siebenecken
erwähnt (siehe unten).
Alle Knotenpunkte sind dreifach und jedes Vieleck hat sieben Nachbarn.
Wir haben aber gezeigt, dass die mittlere Zahl der Nachbarn für Karten mit
dreifachen Knotenpunkten beträgt
N(3) = 6.
Ist das ein Paradox oder ein Gedankenfehler?
Das
mittlere Siebeneck ist von einem Ring von sieben Siebenecken (Heptagons)
umgeben.
Der zweite Ring besteht aus 21 Siebenecken, der dritte aus 56, der vierte aus 147,
dann 385, 1008 und so weiter.
Wie viele Siebenecke beinhaltet der n-te Ring?
* * *
Das
ist nicht alles! Die Ebene kann man auf gleiche Weise mit konvexen Achtecken bedecken.
Hier
jedes Achteck (Oktagon) hat acht Nachbarn. Wie groß ist die mittlere Zahl der Nachbarn?
- etwa 8. Kann das stimmen?
Der erste Ring besteht aus 8
Achtecken,
der zweite
aus
32, der dritte aus 120, dann 448, 1672 usw.
Wie viele Achtecke beinhaltet der n-te Ring?
Analog
ist es mit konvexen Neun-, Zehn- und weiteren N-Ecken!
Ist also die mittlere Zahl der Nachbarn N(3) eine beliebig große natürliche
Zahl?
Auch Bedeckungen der Ebene dieser Art mit zwei verschiedenen Polygonen sind möglich. Hier ein Beispiel mit Hepta- und Hexagonen:
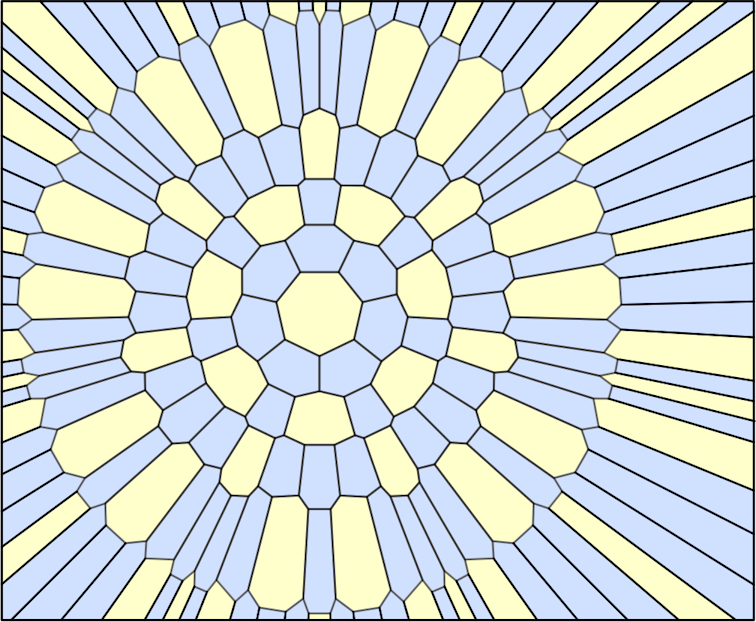
Bemerkung:
auf diese Weise kann man die Ebene mit konvexen Fünfecken nicht bedecken!
Mit Sechsecken ist es möglich:
Zum Vergleichen die reguläre Parkettierung:
* * *
Anzahl der Vielecken in Ringen
Stand: 21.04.2015 / Update 10.04.2018
© Tadeusz E. Dorozinski
im August 2012