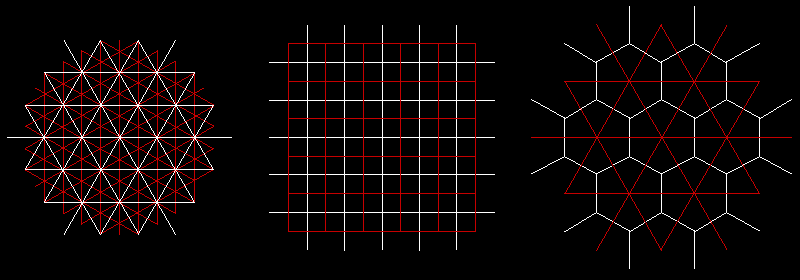
d = 3,4641 d = 2 d = 1,1547
Reguläre und halbreguläre 2D-Netze und Kreislagerungen
3.1. Reguläres Netz mit der kleinsten Dichte
3.2. Dreiecksnetz und seine Unternetze
4. Einige reguläre spezielle Parkettierungen
5. Reguläre und halbreguläre Parkettierungen
6. Parkettierungen mit Zentralsymmetrie
8. Ringe (pierścienie)
2D-Netze sind unendliche Gebilde
in der Ebene. Sie sind aus Knotenpunkten und deren Verbindungen
konstruiert.
Interessant sind vor allem deren gleichmäßige Formen, also
die Netze mit gleichen Knotenverbindungen.
Solche Netze haben viel Gemeinsames mit der Parkettierung der Ebene.
Wenn man in jedem Knotenpunkt ein
Kreis platziert, dessen Durchmesser der Verbindungsstrecke gleich ist,
bekommt man eine feste Kreislagerung in der Ebene
Hinweis:
Die Symmetrieachsen sind
rot gezeichnet.
Die Netz- bzw. Kreislagerungsdichte wird mit d
bezeichnet.

d =
3,4641
d =
2
d = 1,1547
1. 1. Entsprechende
regelmäßige
Kreislagerungen:
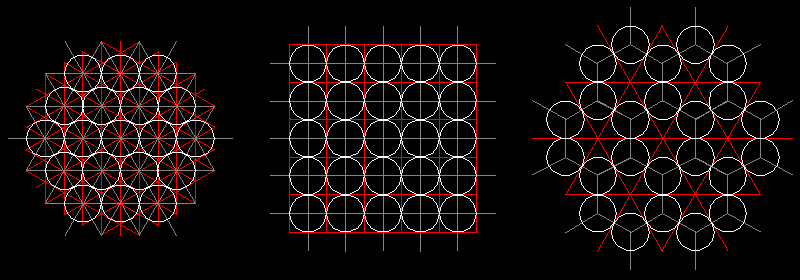
d = 0,9069
d = 0,7854 d =
0,6046
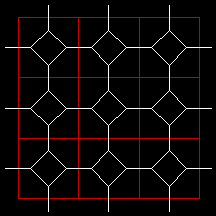
d = 1,0294

d = 1,732
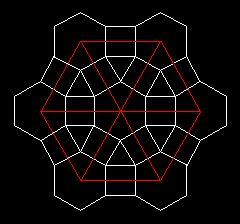
d = 1,8564
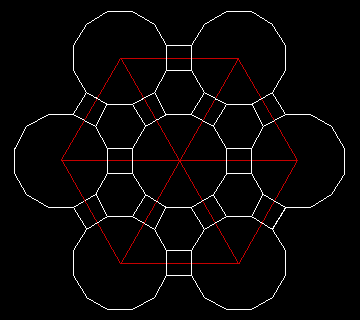
d =
0,9282
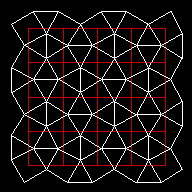
d =
2,6795

d = 2,4743
Die entsprechende Kreislagerung hat die Dichte: d = 0,3907.



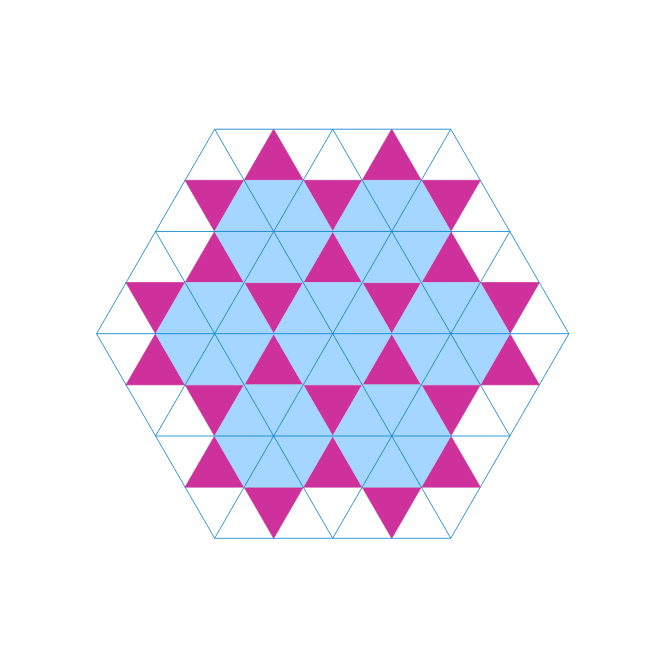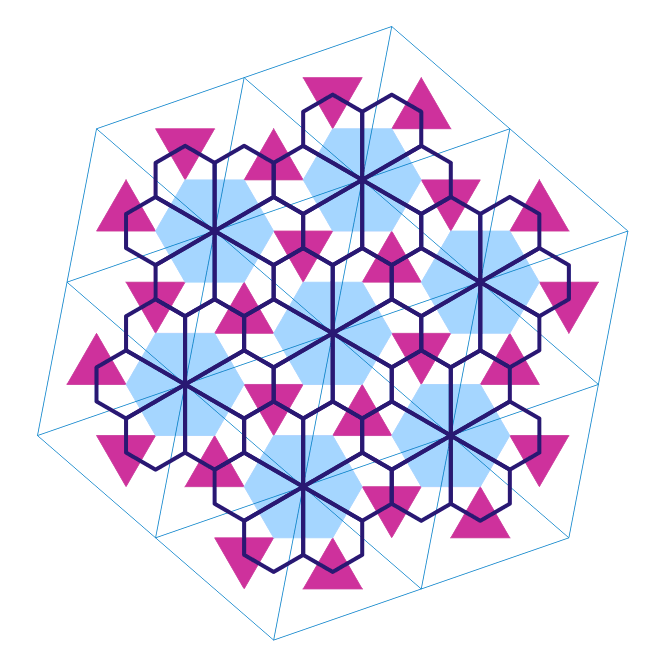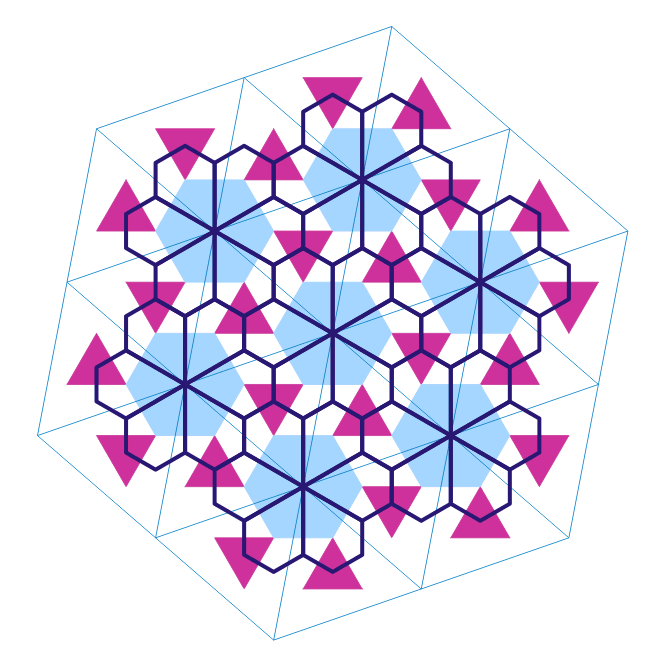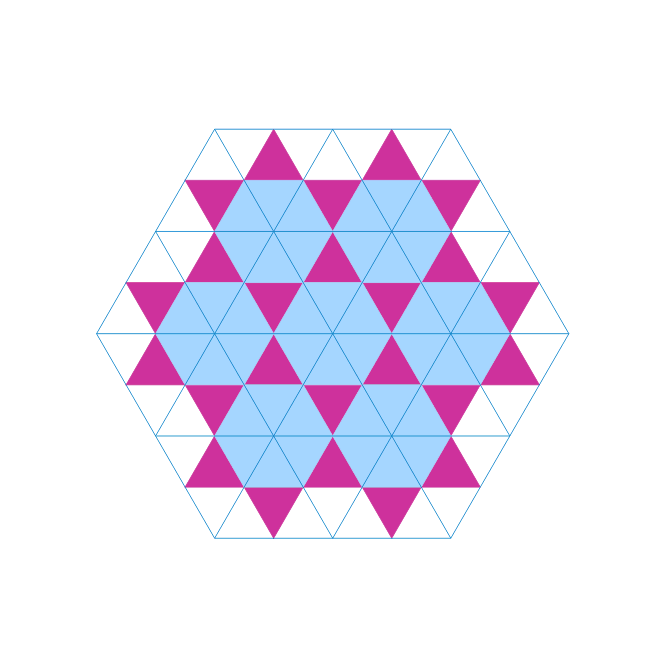
Partkettierung mit Fünfecken
und sein Ableger:
Siehe mehr auf Wikipedia.
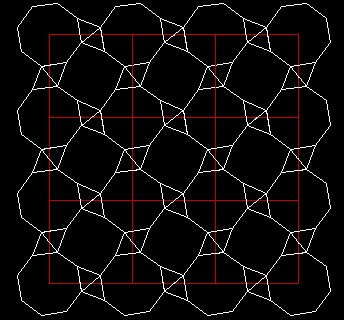
d =
1,2717
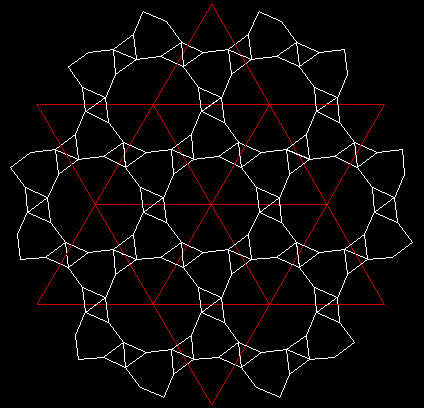
d =
1,1336
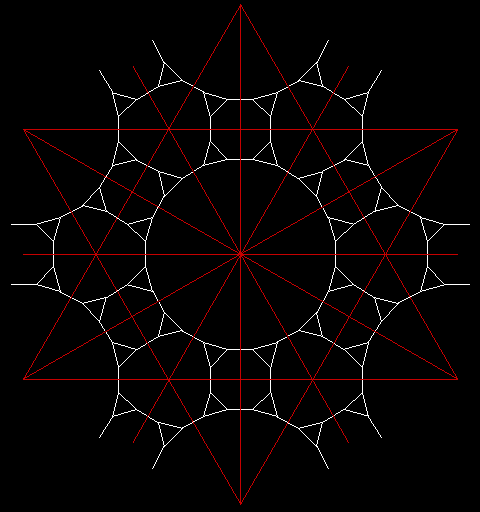
Die entsprechende Kreislagerung hat die Dichte:
d = 0,32583.
Dieses Netz kann man leicht auseinander ziehen (expandieren) um ca. 2%. Die Dichte wird
dann ein wenig kleiner.
Siehe unten !
3.1. Reguläres Netz mit der kleinsten Dichte:
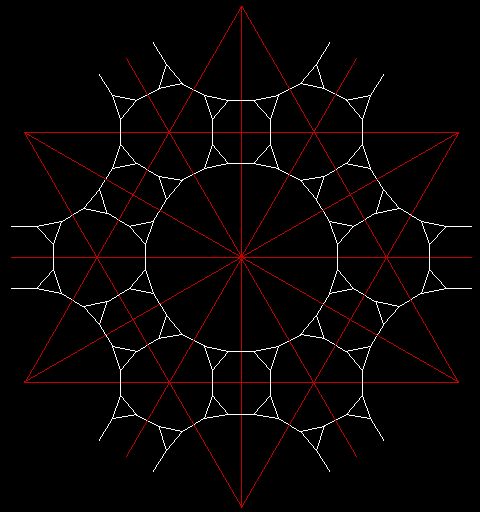
d = 0,6206
Die daraus resultierende Kreislagerung hat die Packungsdichte: d = 0,32495.
Hier die feste Kreislagerung nach der Idee von Enrico Bernal mit der Dichte d = 0,18975 und die entsprechende Parkettierung
und hier andere interessante Kreislagerung von Enrico Bernal mit der Dichte d = 0,4055 und die entsprechende Parkettierung.
4. Einige reguläre spezielle Parkettierungen
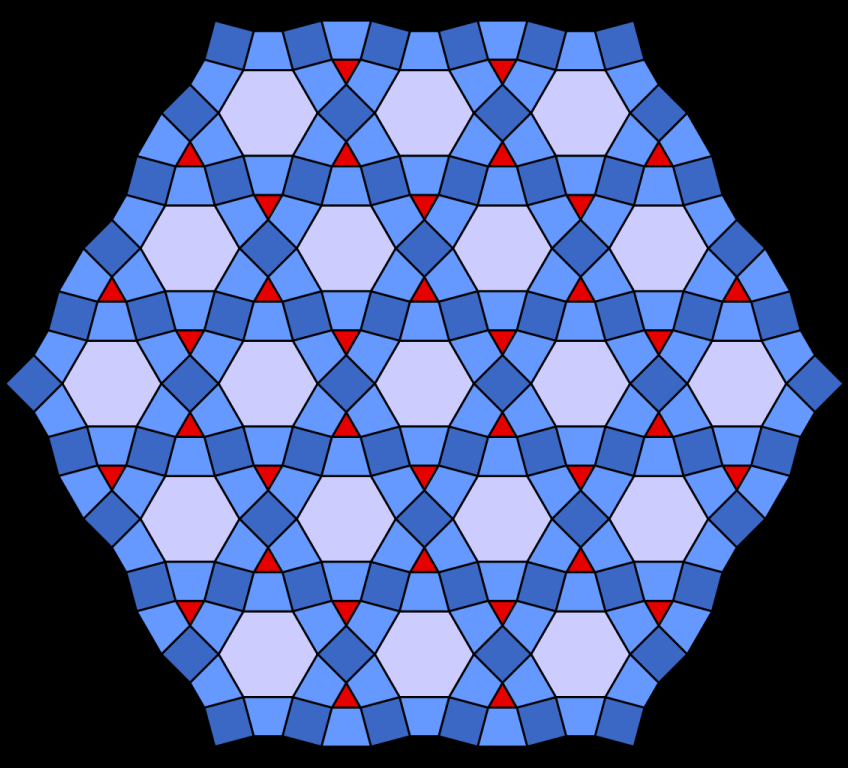





3D/2D-Muster

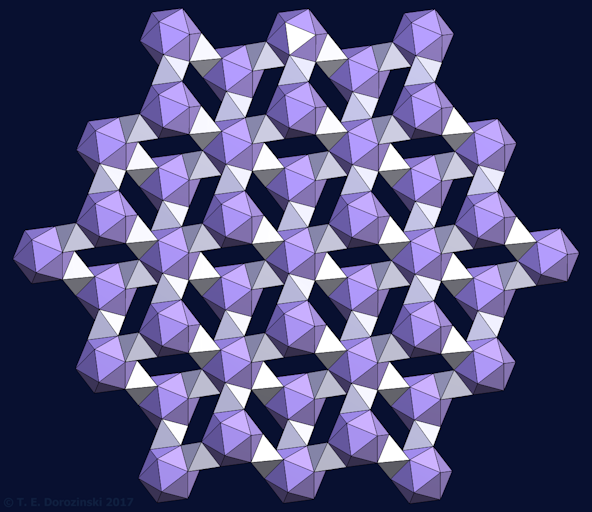



Die bekannte aperiodische Parkettierung von Voderberg. Hier auch farbig im PNG-Format.
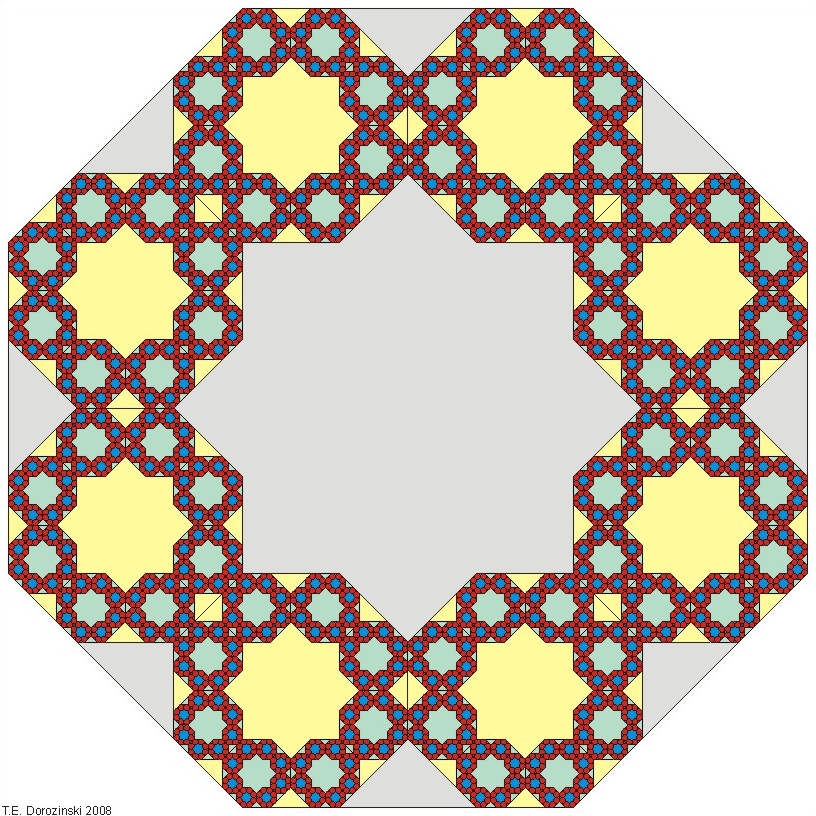
Ein Fraktal aus Achtecken. Iterationsstufe 4
Stand: 08.10.2021
©
Tadeusz E. Dorozinski
E-Mail:
info@3doro.de