Doroids
Doroidal infinite Polyeder
und räumliche, reguläre Polygonstrukturen
Doroids sind infinite Polyeder, die aus
regelmäßigen Polygonen und regulären Polyedern gebaut sind.
Platonische,
Archimedische
und rhombische Polyeder,
als auch reguläre Prismen und Antiprismen
fungieren
als Bauelemente.
Doroids ähneln den regulären unendlichen Poledern (regular skew polyhedra)
und auch ein wenig den toroidalen Polyedern (Toroids),
wo zwei einfache Polyeder "face-to-face" verbunden sind.
Hier, zwei Bauelemente werden "Kante zu Kante" (Edge-to-Edge) oder
"Ecke zu Ecke" (Vertex-to-Vertex) verbunden. Auch Mischformen sind
denkbar.
Die Ecken eines regulären Doroids sollen alle gleich sein (siehe den Beispiel unten).
Achtung: Klick aufs Bild = o2c-Objekt
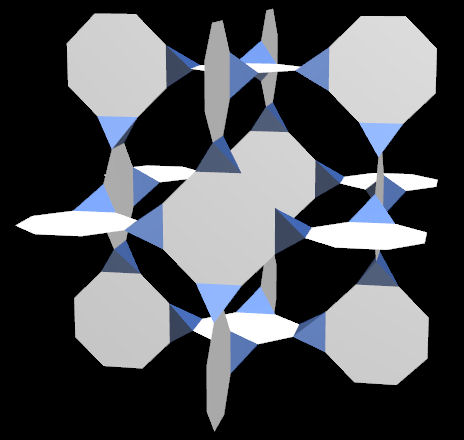
Dieses Doroid ist aus Tetraedern und aus regelmäßigen Oktogons gebaut.
Doroids können als Mittelpunktsfigur von
regulären Kugelpackungen fungieren.
Die Kanten eines Doroids bilden in der Regeln ein reguläres 3D-Netz.
Das war der Grund um die Doroids zu erschaffen.
Doroids vom Typ "Kante zu Kante"

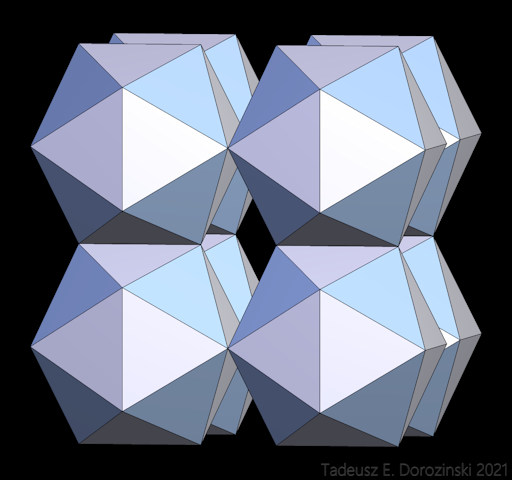
Unten ein Beispiel der Umwandlung eines einfachen Doroids in die Raumfüllung mit Rhombendodekaedern.

12 Dodekaeder platziert auf einem Ikosidodekaeder bilden ein Doroid.
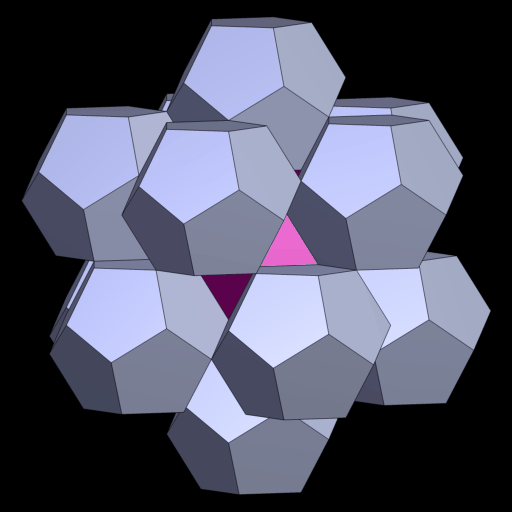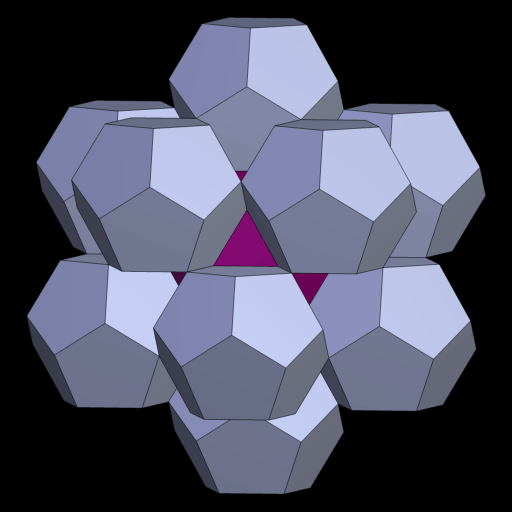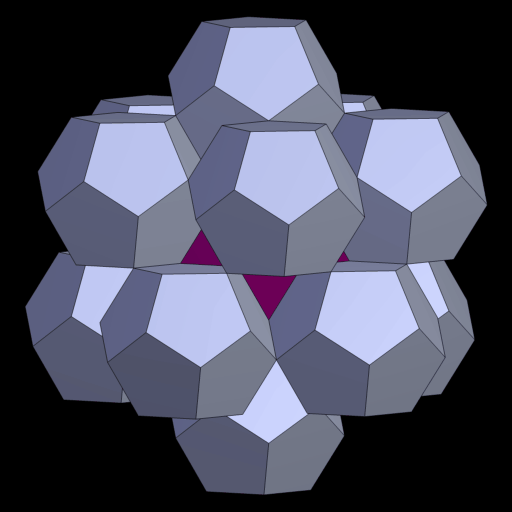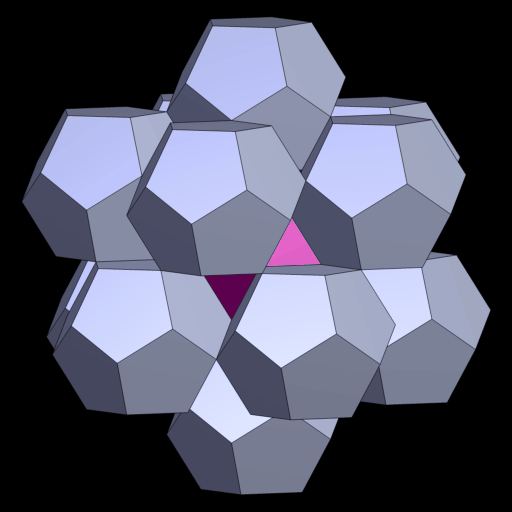
42 Dodekaeder
Auch 20 Ikosaeder bilden ein Doroid.

120 Dodekaeder
120 Ikosaeder
Neueckige Antiprismen


60 Rhomboeder

Doroids vom Typ "Ecke zu Ecke"
Halbreguläre Doroids

Unten noch ein Beispiel der Umwandlung eines einfachen Doroids in die Raumfüllung mit Oktaederstümpfen.


Interpenetration von zwei Doroids
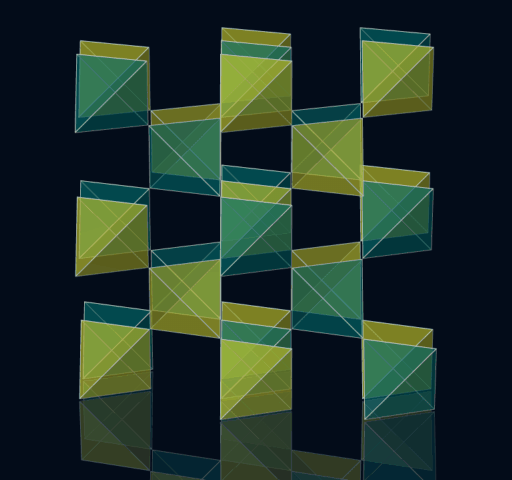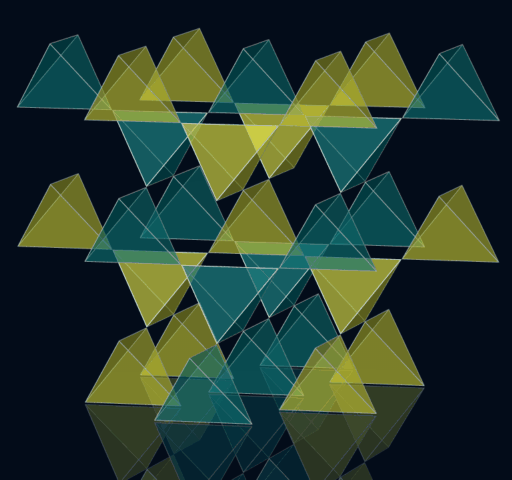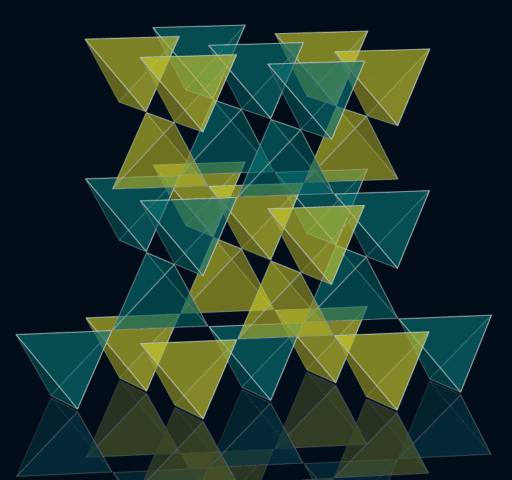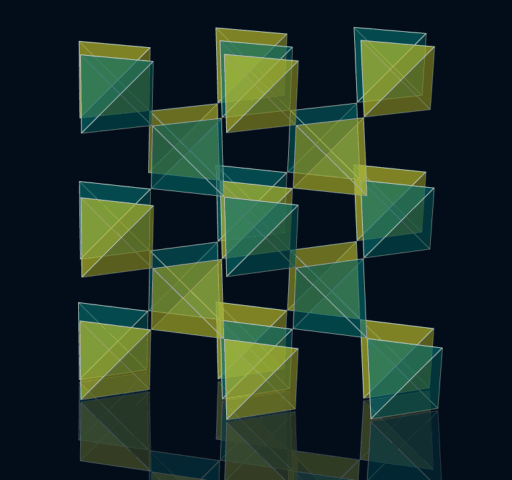
Doroids - Mischformen
Doroids - endliche Formen
Endliche Doroids ähneln mehr den toroidalen Polyedern (Toroids).
Polygone kann man
manchmal zusammenstecken, statt die als "Ecke zu Ecke" anordnen.
Beispiele hier.
Stand: 03.05.2025
© Tadeusz E. Dorozinski, Januar 2012