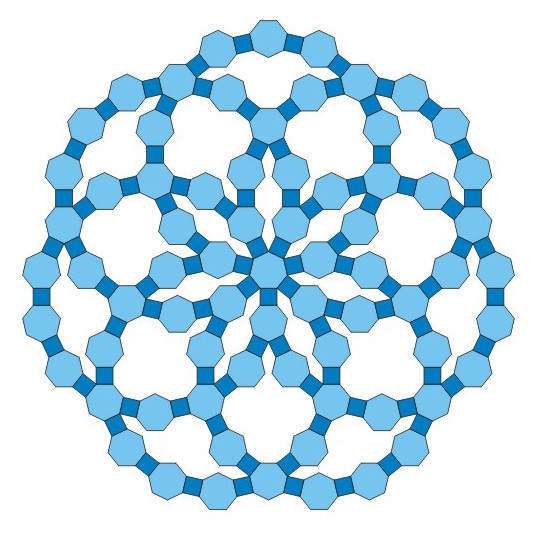
Rys. 1
Pierścieniowe ułożenia wielokątów foremnych na płaszczyźnie
Mając
dowolną ilość jednakowych wielokątów foremnych, np. sześciokątów,
możemy je na różne sposoby regularnie ułożyć na płaszczyźnie.
Możliwe
są ułożenia skończone, jak i nieskończone, np. parkietaże
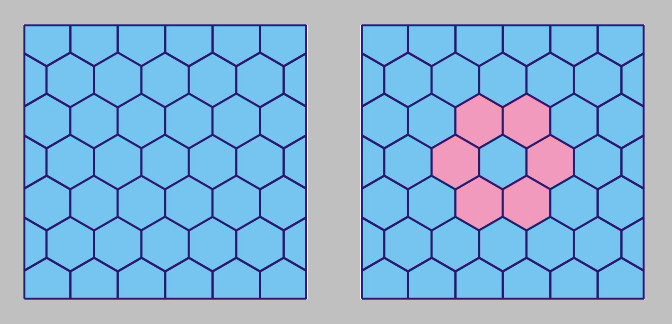
(rys. 1).

Rys. 1
Jak widzimy na rys. 1, w parkietażu sześciokątnym można wybrać sześć sześiokątów, które tworzą regularny pierścień.
Ułożenia skończone w formie regularnych pierścieni zawierają kilka ciekawych aspektów.
Taki
piercień z wieloboków można dla zobrazowania porownać do atolu
na oceanie z laguną w jego wnętrzu.
Każdy wielokąt ma dwa boki wspólne z sąsiednimi wielokątami,
a pozostałe boki stanowią "linię brzegową". Łatwo
zauważyć, że każdy wielobok ma dłuższy brzeg z
"oceanem" niż z "laguną".
Stąd pierwszy wniosek: aby zbudować pierścień, wielokąt
musi być przynajmniej pięciokątem foremnym (dlaczego?).
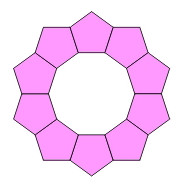
Próba budowy pierścienia z pięciokątów foremnych powiedzie sie (rys. 2).
Rys. 2
Potrzebowaliśmy 10 pieciokątów i wobec tego laguna ma kształt 10-kąta foremnego.
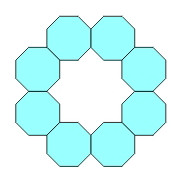
Rys. 3
Na rys. 3 widzimy pierścień zbudowany z ośmiu ośmiokątów foremnych. Tu każdy wielokąt ma dwa boki wspólne z laguną i cztery z oceanem, a laguna jest 16-bokiem gwiaździstym.
Nasuwa się pytanie: jakie pierścienie są możliwe?
Aby na to pytanie odpowiedzieć,
musimy przyjąć pewną systematykę.
Wprowadźmy następujące oznaczenia:
n - liczba boków
wielokąta foremnego,
t - liczba bokow wspólnych wielokąta z laguną.
Liczba ta charakteryzuje typ pierścienia,
k - liczba wielokątów foremnych w pierścieniu.
Te trzy parametry, które są
liczbami naturalnymi, charakteryzują każdy pierscień regularny.
Będziemy więc oznaczać go: n-t-k. Zatem pierscień z rys.
2 ma oznaczenie 5-1-5, a z rys. 3 8-2-16.
Liczba boków laguny jest iloczynem k i t.
Dla możliwych pierścieni zachodzą następujące zależności miedzy tymi trzema parametrami:
(1) t < (n-2) / 2
(2) k = 2n / (n-2t-2) przy czym k ≥ 3, n ≥ 2t+3 i n ≤ 6t+6
Z zależnosci (1) i (2) wynika,
że istnieją cztery pierścienie typu 1 (Rys.
4), sześć pierścieni typu 2 (Rys.
5), pięć typu 3
(Rys. 6), sześć
typu 4, siedem typu 5 itd.
Znajdziemy je rozwiązując równanie (2) w liczbach naturalnych.
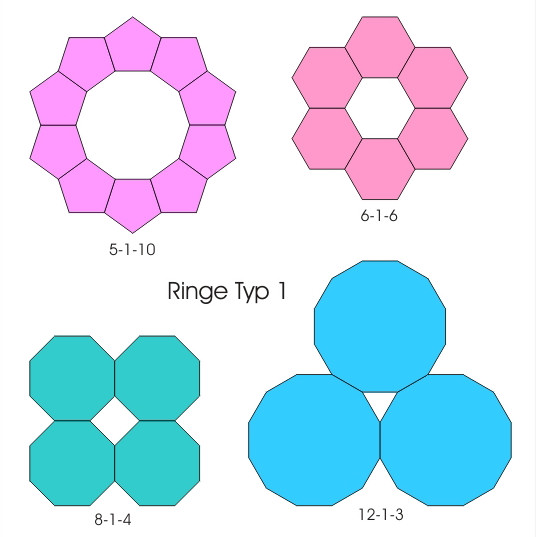
Rys. 4
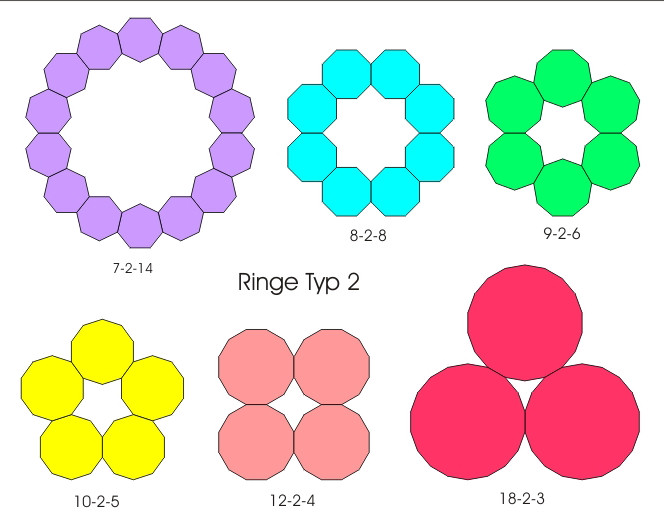
Rys. 5
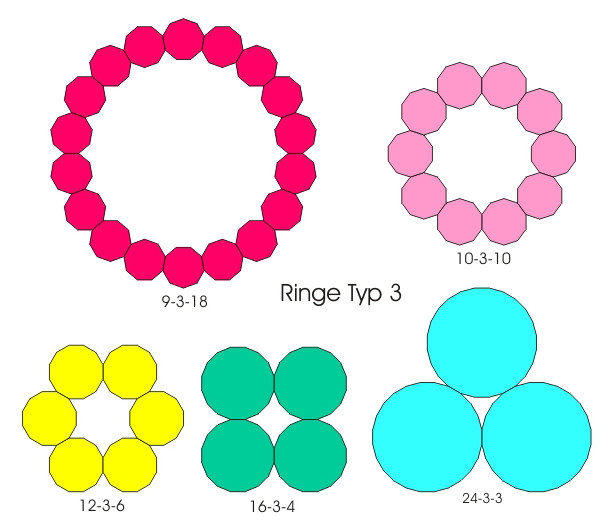
Rys. 6
Poniżej tabela z wartościami k dla t od 1 do 5 i dla n od 5 do 36
| k = 2 n / (n - 2 t + 2) | ||||||
| t | ||||||
| 1 | 2 | 3 | 4 | 5 | ||
| n | 5 | 10 | ||||
| 6 | 6 | |||||
| 7 | 14/3 | 14 | ||||
| 8 | 4 | 8 | ||||
| 9 | 18/5 | 6 | 18 | |||
| 10 | 10/3 | 5 | 10 | |||
| 11 | 22/7 | 22/5 | 22/3 | 22 | ||
| 12 | 3 | 4 | 6 | 12 | ||
| 13 | 26/7 | 26/5 | 26/3 | 26 | ||
| 14 | 7/2 | 14/3 | 7 | 14 | ||
| 15 | 10/3 | 30/7 | 6 | 10 | ||
| 16 | 16/5 | 4 | 16/3 | 8 | ||
| 17 | 34/11 | 34/9 | 34/7 | 34/5 | ||
| 18 | 3 | 18/5 | 9/2 | 6 | ||
| 19 | 38/11 | 38/9 | 38/7 | |||
| 20 | 10/3 | 4 | 5 | |||
| 21 | 42/13 | 42/11 | 14/3 | |||
| 22 | 22/7 | 11/3 | 22/5 | |||
| 23 | 46/15 | 46/13 | 46/11 | |||
| 24 | 3 | 24/7 | 4 | |||
| 25 | 10/3 | 50/13 | ||||
| 26 | 13/4 | 26/7 | ||||
| 27 | 54/17 | 18/5 | ||||
| 28 | 28/9 | 7/2 | ||||
| 29 | 58/19 | 58/17 | ||||
| 30 | 3 | 10/3 | ||||
| 31 | 62/19 | |||||
| 32 | 16/5 | |||||
| 33 | 22/7 | |||||
| 34 | 34/11 | |||||
| 35 | 70/23 | |||||
| 36 | 3 | |||||
Ułamkowe wartości k prowadzą
do pierścieni, w których wieloboki wielokrotnie nakrywają się częściowo.
Tabela zawiera kilka odsyłaczy z przykładami.
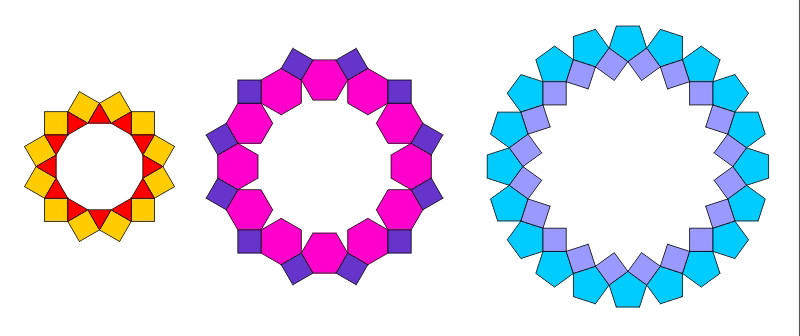
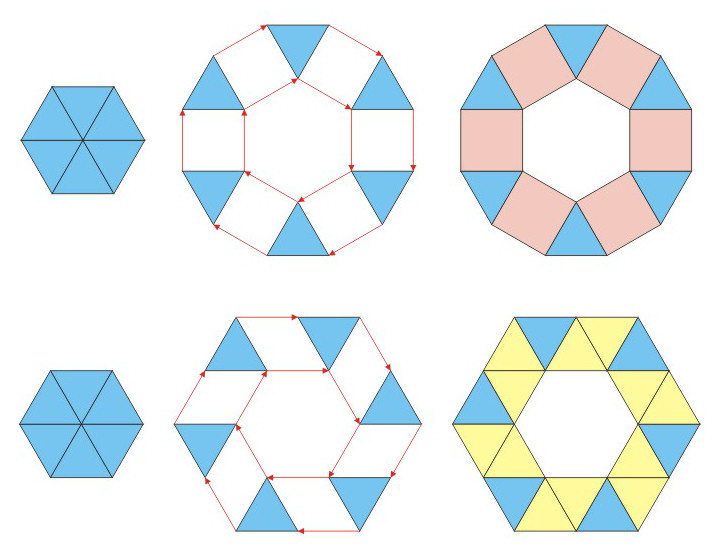
© Tadeusz E. Dorozinski
E-Mail: info@3doro.de
Stand: 15.01.2008