
Einfluss des Standorts (Standpunktes) auf Perspektive
Beim Fotografieren haben wir normalerweise die freie Wahl des Standpunktes und der Brennweite am Fotoapparat. Diese Wahl entscheidet über die Qualität der Aufnahme. Vor allem hat sie Einfluss auf die perspektivische Abbildung.
Unten haben wir einige Beispiele mit verschiedenen Entscheidungen bei der Wahl des Standpunktes und der Brennweite.
Auf dem ersten Bild haben wir eine allgemeine Aufnahme eines Innenhofes, die mit einem normalen Objektiv (die Brennweite - 40 mm) gemacht wurde. Der waagerechte Sehwinkel beträgt ca. 50°. Korrekt sollte man das Bild aus der Entfernung von ca. 18 cm betrachten.

Wenn wir auf dem Bild die Fontäne größer sehen wollen, dann können wir am einfachsten näher an sie heranzoomen. Auf dem Bild unten sehen wir eine Aufnahme mit der Brennweite von 55 mm. Die Perspektive auf beiden Bilder ist gleich. Man kann auch das untere Bild als vergrößerten Ausschnitt des ersten Bildes betrachten. Die korrekte Entfernung beim Betrachten dieses Bildes beträgt ca. 24 cm, also ist es angenehmer.

Die andere Möglichkeit ist die Änderung des Standpunktes zum Fotografieren - näher zu der Fontäne. Die Brennweite brauchen wir dann nicht zu ändern. Eine Aufnahme mit dieser Option sehen wir unten.

Es ist auffallend, dass die perspektivische Abbildung sich stark verändert hat.
Welche Aufnahme ist besser? - dass ist die Geschmacksache.
Hinweis: hier kann man das Prinzip der Konstruktion des Kreises in der Perspektive sehen.
Porträtierung
Unten haben wir zwei Porträts von Nofretete. Das erste wurde mit einem Weitwinkelobjektiv von Nah aufgenommen, das zweite mit einem Teleobjektiv aus größeren Entfernung. Die Unterschiede in der Qualität der Abbildung sprechen für sich.
Man sollte das erste Bild aus ca. 16 cm Entfernung betrachten, das zweite - aus ca. 60 cm.


Die kleine Animation unten zeigt die Unterschiede der Aufnahmen bei einigen Brennweiten von 35 bis 180 mm.

Das Porträtieren hat gewisse Ähnlichkeiten mit Betrachten und mit Fotografieren von Drehkörpern.
Nehmen wir als Beispiel eine Kugel. Es herrscht allgemeine Meinung, dass beim Anschauen einer Kugel - die uns zugewandte Halbkugel sichtbar ist. Die andere Halbkugel bleibt unsichtbar. Das stimmt fast 100-prozentig, wenn wir den Mond (beim Vollmond) anschauen. Der befindet sich jedoch in sehr großen Entfernung zu Erde. Wie ist es aber bei einer Kugel, die wir aus Nähe betrachten (fotografieren)?
Auf der Zeichnung unten ist so eine Situation schematisch dargestellt. Das Auge bzw. die Kamera befindet sich im Punkt S (der Standpunkt). Die Sehstrahlen bilden einen Kegel, der die Kugel berührt. Der Tangentialkreis teilt die Kugeloberfläche in zwei Teile. Der vordere Teil (hellblau dargestellt) ist für uns sichtbar. Das ist eine Kugelkappe mit der Höhe h.
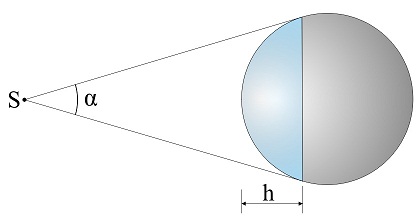
Bezeichnen wir den Öffnungswinkel des Kegels mit α. Es ist leicht zu merken, dass bei wachsender Entfernung des Punktes S und der Kugel, der Sehwinkel α ist kleiner, dafür die Höhe der sichtbaren Kugelkappe h größer. Es ist also fast paradoxal, dass wenn wir von einer Kugel mehr Oberfläche sehen wollen, dann sollen wir uns von ihr entfernen!
Nur wenn der Punkt S unendlich weit liegt, dann die sichtbare Kugelkappe deckengleich mit der Halbkugel ist. Das Verhältnis der Oberfläche der sichtbaren Kugelkappe zu Halbkugel lässt sich aus einfacher Formel berechnen:
V = 100·(1 - sin α/2),
wobei der Sichtbarkeitsgrad V in Prozenten
ausgedrückt wird (V wie Visibilität).
So erhalten wir für
den Winkel
α = 30˚ V
gleich ca. 75%. Da der Sehwinkel des Mondes aus der Erde etwa halben Grad
beträgt, dann sehen wir im Endeffekt ca. 99% der uns
zugewandten Seite (Halbkugel).
Ähnliche Probleme haben wir beim Betrachten anderen Drehkörpern. Da der menschliche Kopf mehr oder weniger rund ist, soll er grundsätzlich aus größerer Entfernung fotografiert werden, sonst kann es passieren, dass beim Verwenden eines Weitwinkelobjektivs der abgebildeten Kopf keine Ohren aufweist!
Stand: 26.09.2021
Erstellt:
23.12.2010
©
Tadeusz E. Dorozinski
E-mail:
info@3doro.de