Geradenbüschel und Kegelschnitte

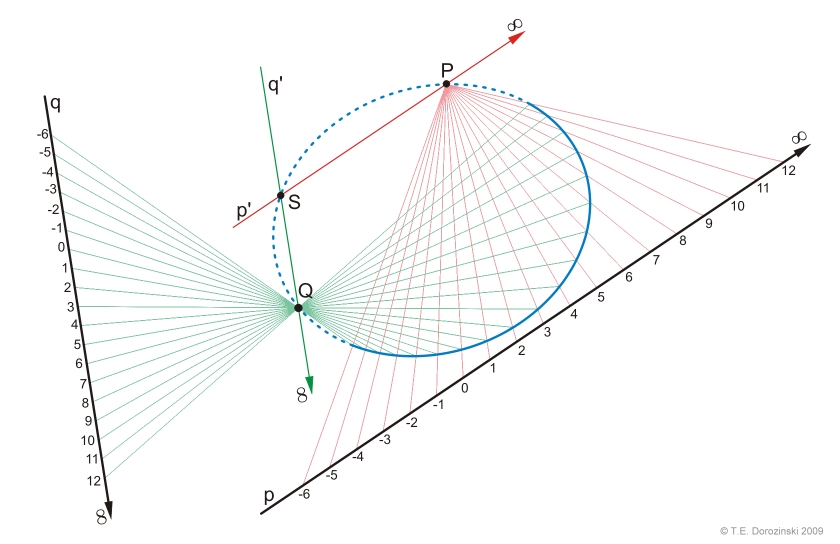
Auf zwei beliebigen Gerade p und q wurden Teilpunkte markiert und nummeriert. Aus zwei punkten P und Q wurden zwei Geradenbüschel entsprechend gebildet.
Die Schnittpunkte vom jeden Geradenpaar mit gleichem Nummer liegen auf einer Kegelschnittkurve. Auf dem Bilde oben ist es eine Ellipse.
Auch Punkte P und Q liegen auf dieser Ellipse, so wie Punkt S - der Schnittpunkt der Geraden p' und q' , die entsprechend parallel zu Geraden p und q sind.

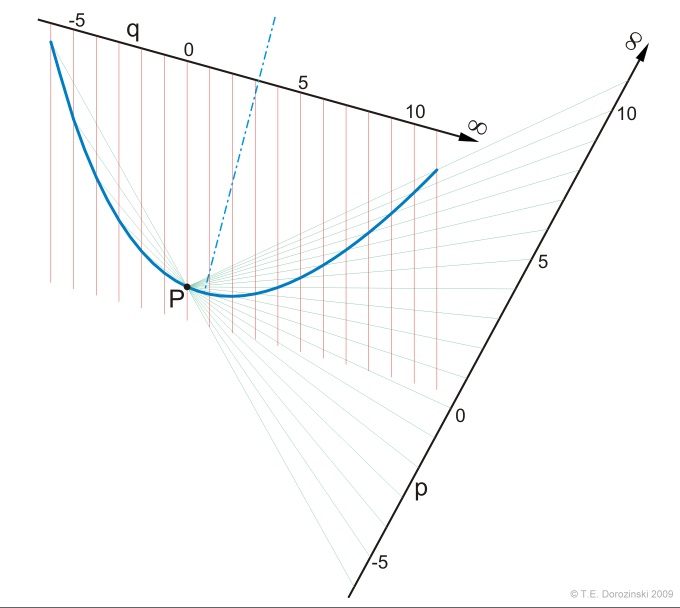
Nehmen wir einer der Punkte P oder Q als Fernpunkt (unendlich weit), dann der Geradenbüschel nimmt die Form eines Geradenbündels an und wir erhalten eine Parabel.

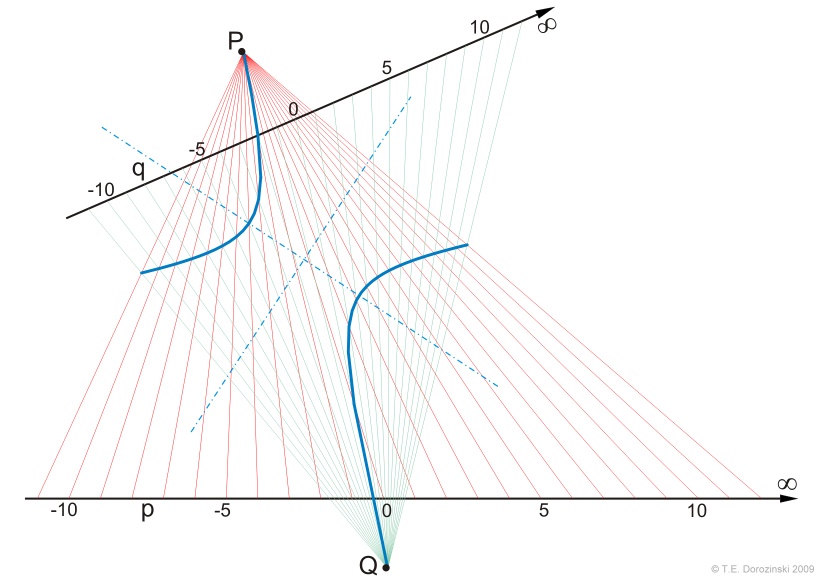
Man kann auch eine Hyperbel bei entsprechender Konfiguration der Geraden und Punkten bekommen.

© Tadeusz E. Dorozinski