Denkaufgaben
1. Zwei Polyeder
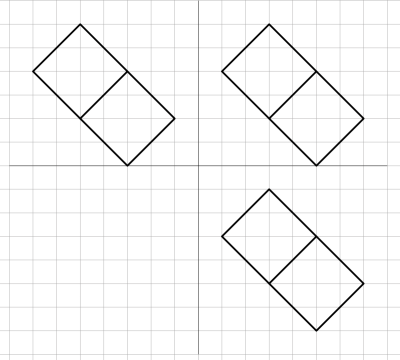
Unten sehen wir Dreitafelprojektionen von zwei Polyedern.

Wie sehen diese Polyeder aus?
* * *
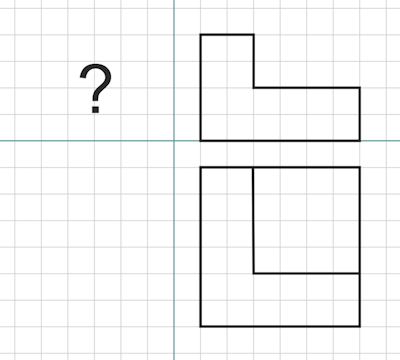
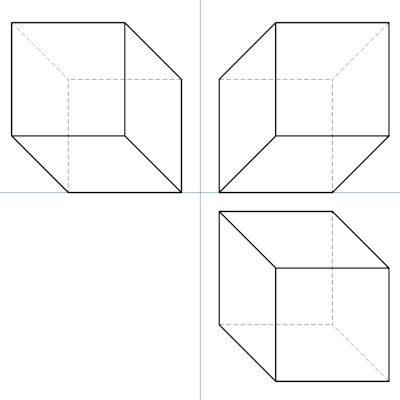
Hier eine alte Aufgabe um das räumliche Vorstellungsvermögen zu trainieren.
In dieser Dreitafelprojektion fehlt die Seitenansicht. Wie sieht sie aus? Bemerkung: alle Kanten von diesem Körper wurden gezeichnet.
Die Lösung kann ich auf Wunsch mitteilen.
2. Zehn Strecken
Hugo Steinhaus* hat vor Jahren diese Aufgabe gestellt:
Zeichnen wir in der Ebene ein beliebiges konvexes Viereck
mit seinen Diagonalen. So erhalten wir fünf Punkte und ihre gegenseitige
Abstände.
Kann man es so tun, dass alle zehn Abstände verschieden und ganzzahlig sind?
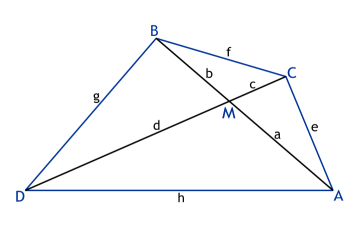
Diese Aufgabe ist leich zu lösen, wenn die beide Diagonale senkrecht zueinander stehen. Dann kann man entsprechende Pythagoreische Tripel finden z. B. so:
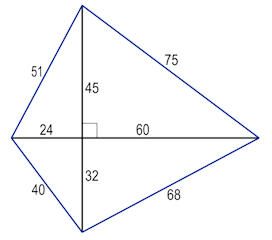
Diese Aufgabe ist viel schwieriger, wenn der Winkel
zwischen beiden Diagonalen nicht 90° ist.
Noch schwieriger wird die Variante mit dem Sechseck, dessen drei Diagonale sich
in einem Punkt M schneiden. Dann haben wir mit 15 Strecken zu tun.
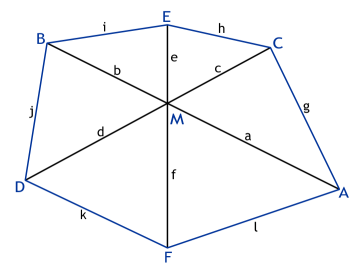
Die beide Aufgaben sind lösbar!
Ich habe beide Lösungen vom Herrn Enrico Bernal aus Stuttgart erhalten.
Hinweis:
Hilfreich sind hier
Dreiecke mit einem Winkel von 60°.
Georg Wengler hat in
GeoGebra einige ganzzahlige Tripel hier
gezeigt-
* siehe: Hugo Steinhaus "100 neue Aufgaben", Urania Verlag (DDR) 1973
3. Drei rhombische Prismen
Wir haben drei rhomische Prismen, deren Achsen sich in einem Punkt schneiden und sind senkrecht zueinander. Die Prismen haben goldene Rhomben als Grundflächen.

Frage: wie sieht der gemeinsame Teil (der Kern) der drei Prismen aus?
Etwas schwieriger ist der ähnliche Fall mit drei Disphenoids. Die sind in einen Tetraederstumpf eingeschrieben.

Wie sieht hier der Kern aus?
4. Die Halbierung des Würfels
Es ist sehr einfach einen Würfel in zwei gleiche (kongruente) Teile zu teilen. Man kann das auf unendlich viele Weisen tun. Beide Hälften können einfach oder komplex sein. Beispiele:
Beide Beispiele unten: K-Dron und D-Dron.
Frage: kann man ein Kubus so halbieren, dass beide Teile chiral sind?
5. Ein Polyeder mit 16 Seitenflächen

Frage: wie entsteht dieses Polyeder am einfachsten?
6. Ein Sechseck im Raum
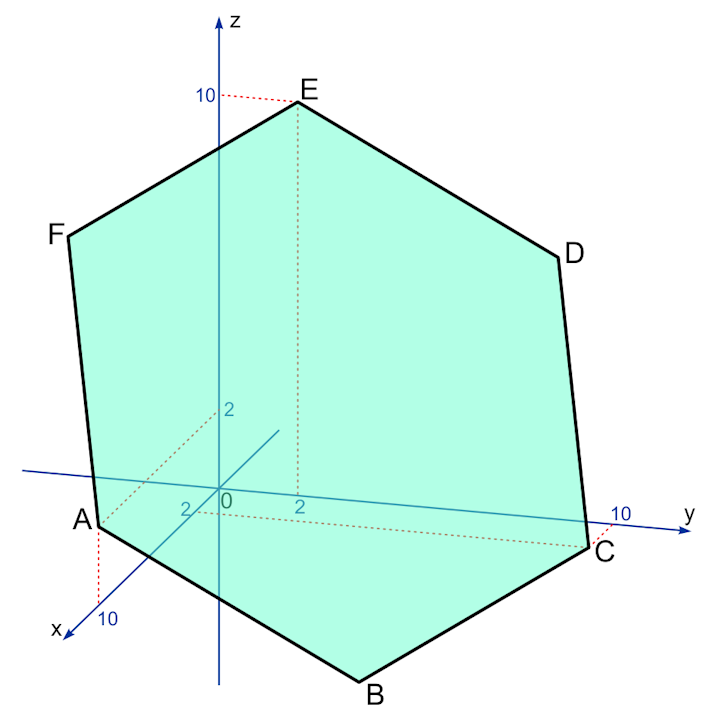
Gegeben ist im Raum ein regelmäßiges Sechseck ABCDEF. Die Koordinaten von drei Ecken sind bekannt: A (10, 0, 2), C (2, 10, 0) und E (0, 2, 10). Bestimmen Sie im Kopf die Koordinaten von Ecken B, D und F.
An Lösungen interessiert? - schreiben Sie mir eine E-Mail.
Stand: 10.06.2021