 STEL
STEL1. Reguläre nicht konvexe Deltaeder
Das sind sehr interessante Gebilde. Die Vielfalt der Formen von nicht konvexen, regulären Deltaedern ist enorm groß. Sie bereichern unsere Fantasie und unseres Raumvorstellungsvermögen.
1.1 Mit tetraedrischer Symmetrie
1.2 Mit oktaedrischer Symmetrie
1.3 Mit pyritoedrischer Symmetrie
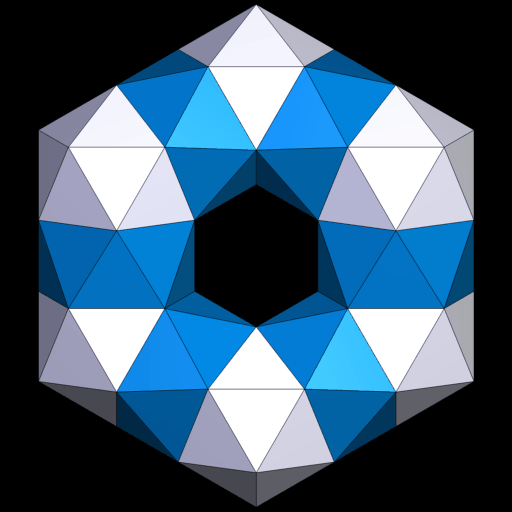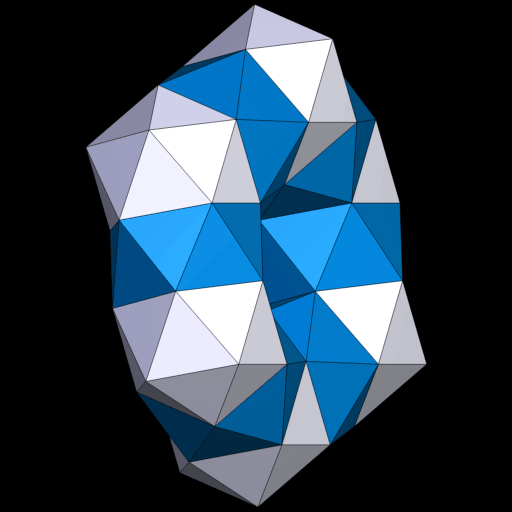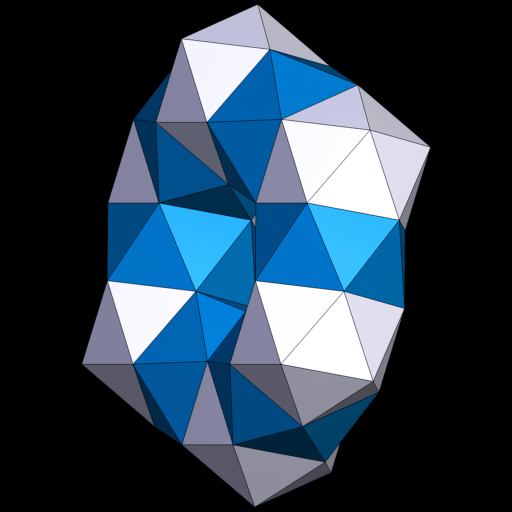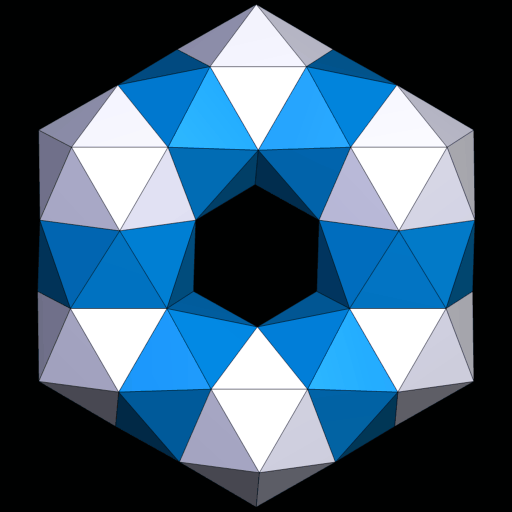
1.4 Mit ikosaedrischer Symmetrie
Das Deltaeder mit 1220 Dreiecken
gefunden von Paul Gailiunas.
Der Artikel von Paul
Gailiunas als PDF
Die kleinere Version mit 740 Dreiecken.
Die kleinere Version mit 380 Dreiecken.
Ein Deltaeder mit der tetraedrischen Symmetrie:
2. Reguläre, infinite nicht konvexe Deltaeder


3. Reguläre, toroidale nicht konvexe Deltaeder
Ein mehrschichtiges Toroid aus 7600 Dreiecken- Genus 149.
4. Beweglichkeit der nicht konvexen Deltaedern
Goldberg-Ikosaeder. Mehr dazu hier.
STEL-files dazu:
STEL-24a STEL-24b STEL-60a STEL-60b

Mehr dazu hier.
5. Sonstige nicht konvexe Deltaeder
Stand: 06.02.2026
© Tadeusz E. Dorozinski