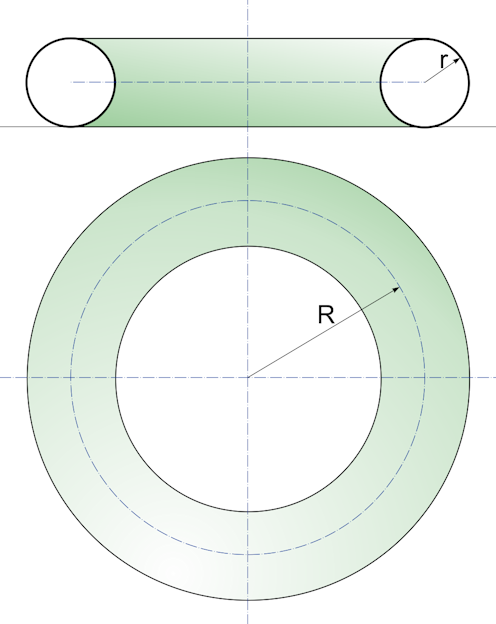
Draufsicht und Schnitt eines Torus
Der Torus wird durch zwei Parameter (Größen) bestimmt: durch den Radius r des rotierendes Kreises und den Mittelkreisradius R.

Draufsicht und Schnitt eines Torus
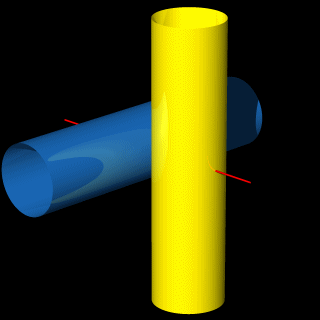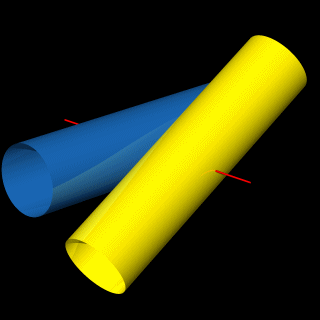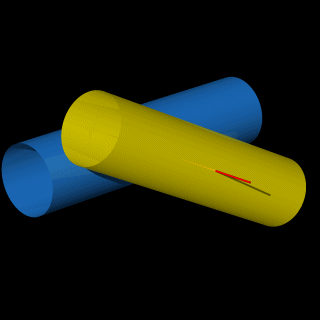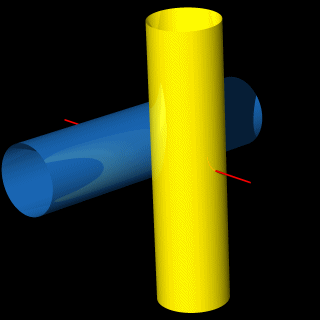
Darunter sehen wir zwei verschlungene (verflochtene), gleiche Tori.
Die beide Tori berühren sich in einem einzigem Punkt, durch den die rote Achse verläuft.
Frage: sind diese beide Tori um die rote Achse drehbar und in welchem Grade?
Es gibt zwei Grenzfälle: in erstem, wo R = 2r und in zweitem, wo R = ∞.
In erstem Fall sind die beide Tori unbeweglich:
In zweitem Fall werden die Tori zu zwei gleichen Zylinder und die sind beliebig drehbar.
Wer kann die hier gestellte Frage beantworten?
1. Hinweis (02.04.2014)
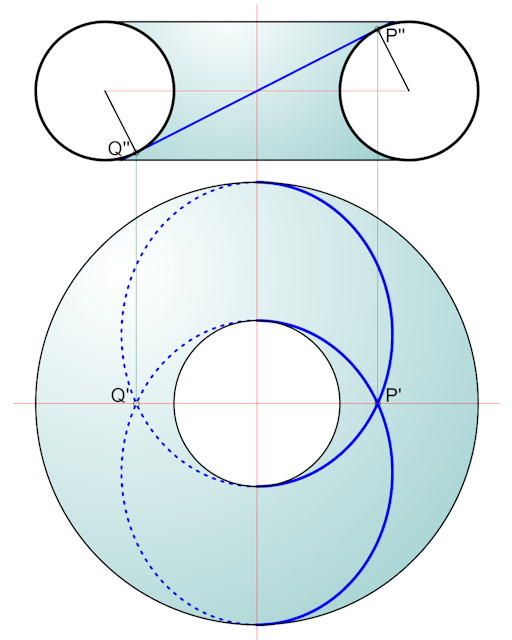
Der Torus-Schitt mit einer
senkrechten Ebene, die den inneren Äquator in einem Punkt berührt, ist eine
Lemniskate.
In solchem Punkt berühren sich die beide Tori.
Ein besonderer Torus-Schnitt - Villarceau-Kreise
Die bekannte Borromäische Ringe. das sind drei langgestreckte Tori. Die lassen sich nicht voneinander trennen.

Aus langgestreckte Tori kann man infinite, reguläre Struktur bauen.
Wie ist es mit 12 langgestreckten Tori in diesem Puzzle?
Lassen sich die 12 Teile
auseinandernehmen?
Ja! Das Beweisfoto.
Jeder kann das selbst überprüfen. Entsprechende 3D-Prints kann man hier
bestellen: Shapeways.
Und hier die Variante des Puzzles im Holz:
Eine Zusammenstellung der Einzelteilen kann ich den Interessierten zur Verfügung stellen.
Reguläre Packungen der gleichen Tori im Raum
So eine unendliche Packung sehen wir auf dem Bild unten.
Durch jeden Torus gehen vier Tori durch. Benachbarte zwei Tori berühren sich in einem Punkt.
Fragen
1. Wenn r =1, dann wie groß ist der Radius R?
2. Zum welchen Grad füllen diese Tori den Raum?
3. Ist das die einzige reguläre unendliche Packung
der gleichen Tori?
Aufgabe
Man kann alle Tori in gleiche Polyeder mit dem Genus 1 so umwandeln, dass
sie den Raum lückenlos ausfüllen.
Wie so ein Polyeder könnte aussehen?
Erstellt: 28.03. 2014
Stand: 02.11.2018
© Tadeusz E. Dorozinski